Software Estimation

Software Estimation
An Introduction

Prof. David Bernstein
James Madison University

Computer Science Department

bernstdh@jmu.edu

Motivation

Some Common Planning Tasks:
- Scheduling
- Budgeting
Required Information:
- Time estimates (perhaps by task)
- Cost estimates
Some Perspective (Standish, 2001; Kidder 1981)
- 63% of successful software development projects are late
- 45% of successful software development projects are over budget

Nerd Humor

(Courtesy of xkcd)

Using Historical Data

Scope:
- Industry-standard vs. organization-specific
Nature of the Data:
- Qualitative (small, medium, large) vs. quantitative (LOC or FP)
Modeling Technique:
- Formal (e.g., use regression analysis to estimate parameters of the model from the data) vs. informal (e.g., identify rules-of-thumb)

An Example - Organization-Specific, Quantitative, Informal

Background Information:
- Function points for earlier products
- A rule-of-thumb about organization-specific productivity in function points per person-months (e.g., 5 FP/pm)
- Labor cost in dollars per person-month (e.g., $12,000/pm)
Information about the Product:
- 425 FPs
Constructing a Point Estimate:
- Effort: $E = 425 / 5 = 85$pm
- Cost: $C = 85 \cdot 12000 = 1020000$dollars

An Example - Industry-Standard, Quantitative, Formal

KLOC-Based ($L$) Log-Linear:
- Walston and Felix (1977): $E = 5.2 L^{0.91}$
- Basili and Freburger (1981): $E = 1.38 L^{0.93}$
- Boehm (1981): $E = 3.2 L^{1.05}$
FP-Based ($F$) Linear:
- Albrecht and Gaffney (1983): $E = -91.4 + 0.255 F$
- Kemerer (1987): $E = -37.0 + 0.96 F$
- (Note that the negative $y$-intercept means that these models are not appropriate for small values of $F$.)

An Example - Organization-Specific, Qualitative, Formal

Data Collection (Humphrey, 1995):
- Classify features from other products as very small, small, medium, large, and very large
- Collect data from other products on LOC per feature (if done correctly, categories should vary by at least a factor of 2)
Estimation:
- Classify required features
- Count the features in each classification
- Multiply
- Add

Some Common Models

The Software Equation:
- $E$ (effort) is a function of $t$ (project duration) and $L$ (KLOC)
COCOMO II:
- $E$ is a function of $L$, $F$ (function points), or object points
International Software Benchmarking Standards Group:
- $E$ is a function of $F$ and $N$ (team size) with specific parameters for different physical architectures and languages

The Software Equation (Putnam and Meyers, 1992)

Additional Notation:
- $t$ denotes the project duration
- $B$ denotes a "special skills factor" ($B$ is 0.16 for products with fewer than 15 KLOC and increases to 0.39 for products with more than 70 KLOC)
- $p$ denotes a "productivity factor" that reflects the process and practices, experience, and product complexity (e.g., 2000 for real-time embedded software, 12000 for scientific software)
The Two-Variable ($L$ and $t$) Model:
- $E = \frac{L \cdot B^{1/3}}{p^3} \cdot \frac{1}{t^4} $
The One variable Model:
- $t = 8.14 \frac{L}{p^{0.43}}$
- $E = 180 B \left(\frac{t}{12}\right)^{3}$

COCOMO II - Constructive Cost Model (Boehm, 1981/2000)

Collection of Models:
- Pre-Requirements (Application Composition)
- Stabilized Requirements (Early Design)
- Construction (Post-Architecture)
Alternative Size Measures:
- Lines of Code
- Function Points
- Object Points
Factors to Consider:
- Scale factors
- Product factors
- Platform factors
- Personnel factors
- Project factors

COCOMO II (cont.)

Nominal Effort:
- $E = 2.94 \cdot L^\beta \cdot \prod_{i=1}^{16} W_i$
- where $W_i$ is an effort multiplier, $\beta = 0.91 + 0.01 \cdot \sum_{j=1}^{5} \Psi_j$, and $\Psi_j$ is a scale factor
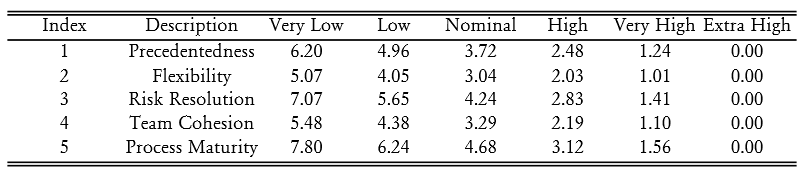
The Scale Factors ($\Psi_j$):
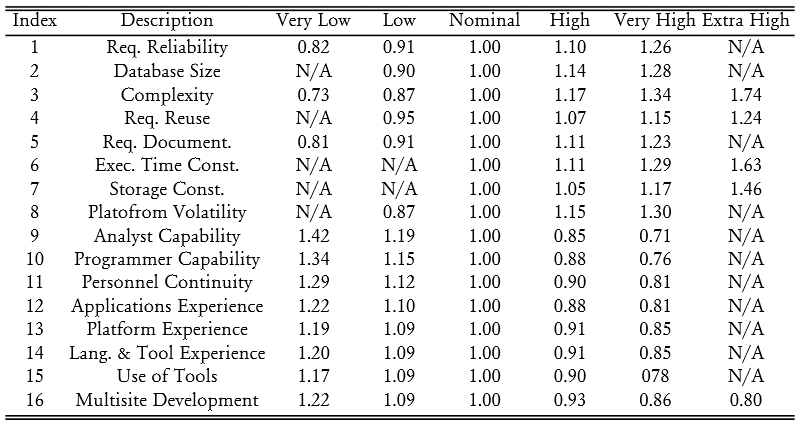
Effort Multipliers ($W_i$):

International Software Benchmarking Standards Group (2005)

Additional Notation:
- $N$ denotes the (maximum) team size
A General Model:
- $E = 0.512 \cdot F^{0.392} \cdot N^{0.791}$
Other Models:
- They have estimated the parameters of this model for products for mainframes, mid-range systems, desktops
- They have estimated the parameters of this model for different kinds of languages