|
Linear Regression
An Introduction |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
|
Linear Regression
An Introduction |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
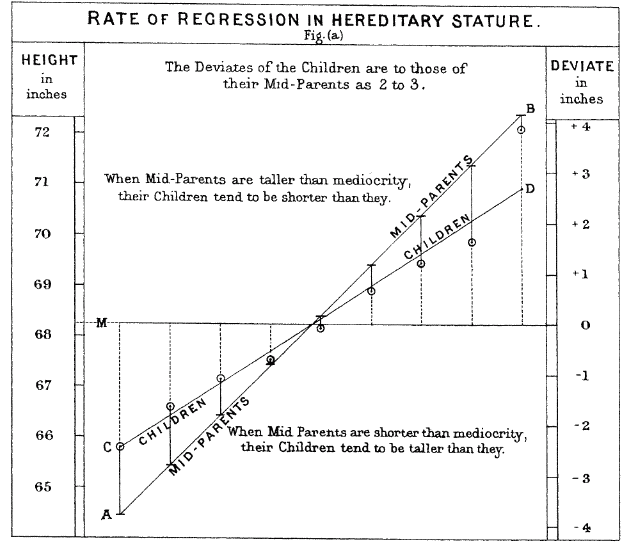
Galton's Data
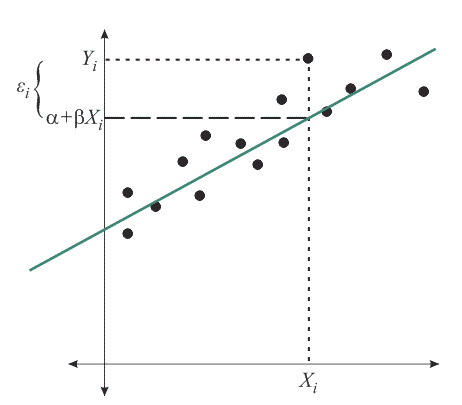
For linear models through the origin (i.e., with just \(\beta\)) we have:
\[ \min \sum_{i=1}^n (Y_i - \beta X_i)^2 = (Y_1 - \beta X_1)^2 + \cdots + (Y_n - \beta X_n)^2 \]
which we need to differentiate, set to 0, and solve.
\[ \frac{d}{d \beta} \sum_{i=1}^{n}(Y_i - \beta X_i)^2 = \frac{d (Y_1 - \beta X_1)^2}{d\beta} + \cdots + \frac{d (Y_n - \beta X_n)^2}{d\beta} \] \[ = 2\cdot-X_1\cdot(Y_1 - \beta X_1) + \cdots + 2 \cdot -X_n \cdot (Y_n - \beta X_n) \] \[ = 2 \sum_{i=1}{n} -X_i \cdot (Y_i - \beta X_i) = 2 \sum_{i=1}^{n} -X_i Y_i + 2 \sum_{i=1}^{n} \beta X_i^2 \]
So, at the minimum:
\[ \sum_{i=1}^n X_i Y_i = \sum_{i=1}^n X_i^2 \]
which implies that, at the minimum, \(\beta = \frac{\sum_{i=1}^n X_i Y_i}{\sum_{i=1}^n X_i^2}\)
For affine models (i.e., with both \(\alpha\) and \(\beta\)) we need to take partial derivatives, set them equal to 0, and solve.
Starting with \(\alpha\):
\[ \frac{\partial}{\partial \alpha} \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i)^2 = 2 \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i) \cdot -1 \] At the minimum: \[ \sum_{i=1}^{n}Y_i - \sum_{i=1}^{n} \alpha - \sum_{i=1}^{n} \beta X_i = 0 \Rightarrow n \cdot \alpha = \sum_{i=1}^{n}Y_i - \beta \sum_{i=1}^{n}X_i \] Dividing by \(n\): \[ \alpha = \overline{Y} - \beta \overline{X} \] where \(\overline{Y}\) and \(\overline{X}\) are the mean of \(Y\) and \(X\) respectively.
Now solving for \(\beta\):
\[ \frac{\partial}{\partial \beta} \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i)^2 = 2 \sum_{i=1}^{n}(Y_i - \alpha - \beta X_i) \cdot -X_i \] At the minimum: \[ \sum_{i=1}^{n}Y_i X_i - \sum_{i=1}^{n}\alpha X_i - \sum_{i=1}^{n} \beta X_i^2 = 0 \Rightarrow \sum_{i=1}^{n}Y_i X_i - \alpha \sum_{i=1}^{n} X_i - \beta \sum_{i=1}^{n}X_i^2 = 0 \] Substituting \(\alpha = \overline{Y} - \beta \overline{X}\) \[ \sum_{i=1}^{n}Y_i X_i - \overline{Y} \sum_{i=1}^{n} X_i + \beta \overline{X} \sum_{i=1}^{n} X_i - \beta \sum_{i=1}^{n}X_i^2 = 0 \] which implies \[ \sum_{i=1}^{n}X_i(Y_i - \overline{Y}) + \beta \sum_{i=1}^{n} X_i (\overline{X} - X_i) = 0 \] Solving for \(\beta\): \[ \beta = \frac{\sum_{i=1}^{n}X_i(Y_i - \overline{Y})}{\sum_{i=1}^{n} X_i (X_i - \overline{X})} \]
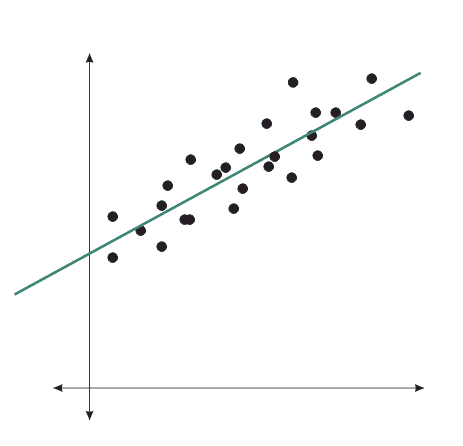 vs.
vs.