Waves
A Brief Introduction
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
Mechanical Waves
- Pulse:
- A single disturbance that moves through
a sequence of interacting particles (called a
medium)
- Periodic Wave:
- A periodic disturbance that moves
through a medium, transporting energy as it moves
Mechanical Waves (cont.)
- Some Observations:
- Individual particles do not
move very far (each particle oscillates around its equilibrium
position, but its average position does not change)
- As a particle interacts with its neighbors it transfers
some of its energy to them, causing them to oscillate
- As this process continues, the
energy is transported throug the medium.
- Common Examples:
- Waves in water (from which you have developed most
of your intuition)
- Waves in a spring (a medium consisting of individual
coils)
Mechanical Waves (cont.)
- One way to generate a wave:
- Move the left end
of the spring "back and forth" in the
horizontal direction
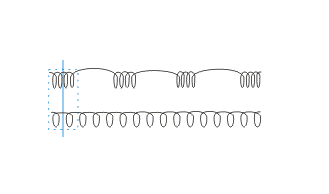
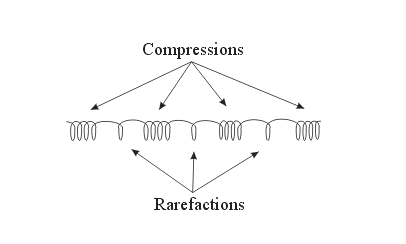
- The result - a longitudinal wave:
- A series of compressions (areas in which the
particles are closer than in equilibrium) and
rarefactions (areas in which the particles are
farther apart than in equilibrium)
-
Mechanical Waves (cont.)
- Another way to generate a wave:
- Move the left end
of the spring "up and down" in the
vertical direction
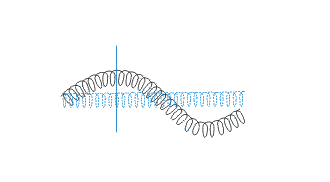
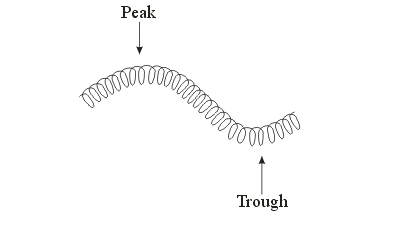
- The result - a transverse wave:
- A series of peaks (areas in which the particles
are "higher" than in equilibrium) and troughs
(areas in which the particles are "lower" than in
equilibrium)
-
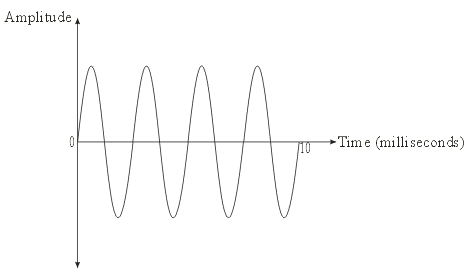
The Position Domain
- Amplitude of a Longitudinal Wave:
The Position Domain (cont.)
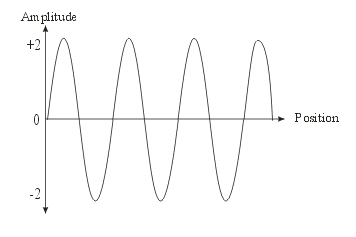
- Amplitude of a Transverse Wave:
The Position Domain (cont.)
- Wavelength (of a periodic wave):
- The distance one has to travel along the wave
until it "repeats"
- Usually denoted by \(\lambda\) (and measured in
some unit of length per cycle)
The Position Domain (cont.)
- Interference:
- When two waves meet while traveling through the same
medium they are said to interfere with each
other
- Principle of Superposition:
- When two waves interfere, the resulting displacement of
the medium at any location is the sum of the
displacements of the individual waves at that same
location
- Types of Interference:
The Time Domain
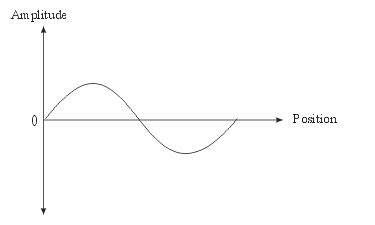
- The Concept:
- The figures above are all plots of the amplitude of the
wave versus the position
- Alternatively we could have picked a particular position
along the wave and looked at how the amplitude at that
position changed over time
- An Example:
The Time Domain (cont.)
- Cycle:
- A portion of a wave from that goes from rest to crest to
rest to trough to rest
- Period:
- The time required for a cycle
- Frequency:
- The reciprocal of the period
(i.e., is the number of cycles per second or hertz)
- Usually denoted by \(f\)
- Speed:
- The product of wavelength and frequency
- Usually denoted by \(v\)
- Thinking about units: \(v = \lambda f\) (e.g.,
m/sec = m/cycle \(\cdot\) cycles/second)
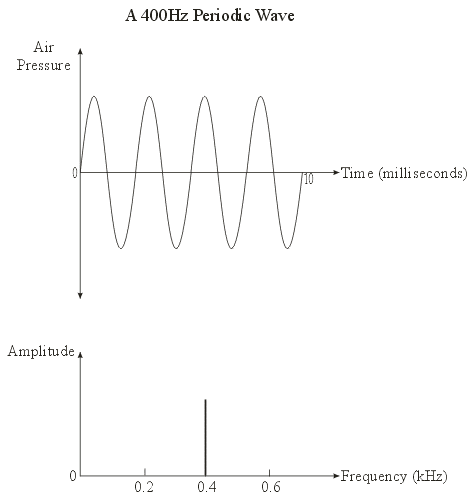
The Frequency Domain
- A 400Hz Periodic Wave:
- Spectra:
- Periodic waves have a line spectrum
- Quasiperiodic waves have
harmonic spectra
- Aperiodic waves have continuous
spectra
The Frequency Domain (cont.)
- The Fourier Transform:
- Can be used to convert from the time domain to
the frequency domain
- Fourier's Discovery:
- All periodic waves may be expressed as the sum of a
series of sinusoidal waves
- These waves are all integer multiples (called
harmonics) of the fundamental frequency
- Each harmonic has its own amplitude and phase
The Doppler Effect
- Defined:
- An increase (or decrease) in the frequency of a wave
as the source and observer move toward (or away from)
each other
- History:
- Described by Christian Doppler in 1842
A Sound Wave Example of the Doppler Effect
- Situation 1:
- The Source: A car 1 mile away, standing still, plays a pure tone
for one minute
- The Observer: Hears nothing for 4.73 secs (while the
wave travels the one mile at 761 mph) and then hears the tone
for one minute
- Situation 2:
- The Source: A car 1 mile away, traveling towards the observer at
60mph, plays a pure tone for one minute
- The Observer: Hears nothing for 4.73 secs (while the
wave travels the one mile at 761 mph) and then hears something
for 55.27 seconds
A Sound Wave Example of the Doppler Effect (cont.)
- Understanding Situation 2:
- It takes the car 1 minute (i.e., 60 seconds)
to travel the mile
- So, the tone stops being played exactly when the car
reaches the observer
- So, the tone stops being played 55.27 seconds after
it is first heard by the observer
- Since the car is located at the observer when the tone stops
playing, the observer stops hearing it exactly when it stops
being played
- Important Observations:
- The tone is being played for 60 seconds but only heard
by the observer for 55.27 seconds
- This means that the same number of waves reach the
observer in a smaller amount of time, which is to say that the
frequency of the waves must have increased
The Doppler Effect (cont.)
- Notation:
- \(f_o\) denotes the observed frequency
- \(f_e\) denotes the emitted frequency
- \(v_w\) denotes the velocity of the wave in the
medium
- \(v_s\) denotes the velocity of the source
- One Case:
- The source is moving towards the observer
- The observer is stationary
- The Relationship:
- \(f_o = \frac{v_w}{v_w - v_s} f_e\)
The Doppler Effect (cont.)
- Data from the Example:
- \(v_w = 761\)
- \(v_s = 60\)
- Implication:
- \(f_o = \frac{761}{761 - 60} f_e = 1.08 \cdot f_e\)
The Doppler Effect (cont.)
An Illustration

Source: Wikimedia