|
Vector Mathematics in 2D
An Introduction to 2D Vectors |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
|
Vector Mathematics in 2D
An Introduction to 2D Vectors |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
Points
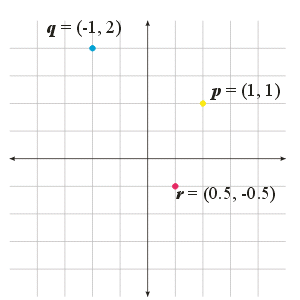
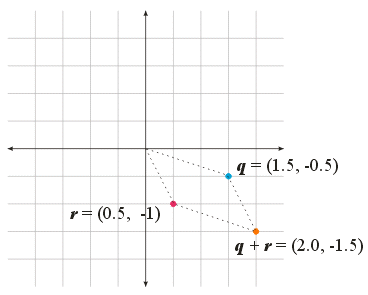
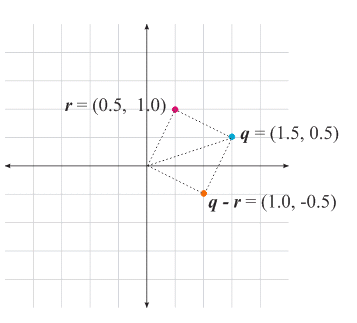
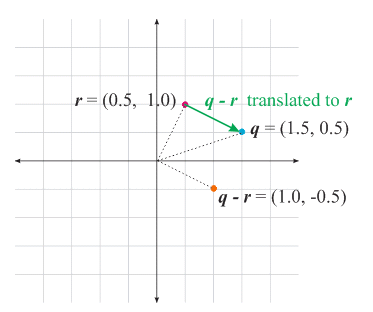
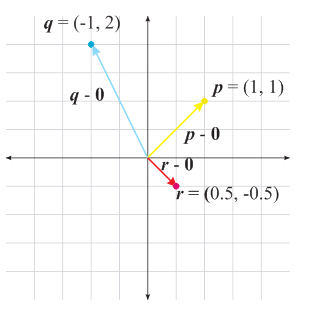
We will use the different visualization techniques in different situations. So, you will have to be very careful.
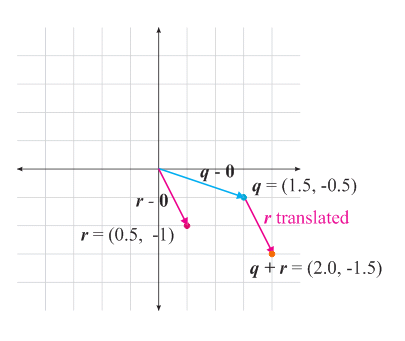
Visualization
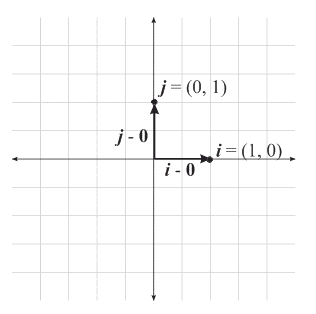
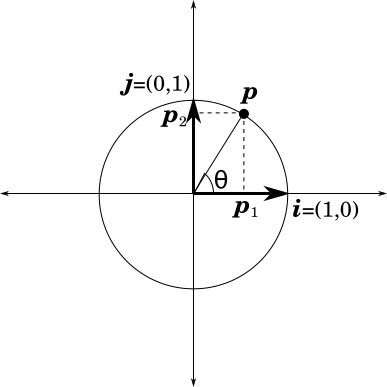
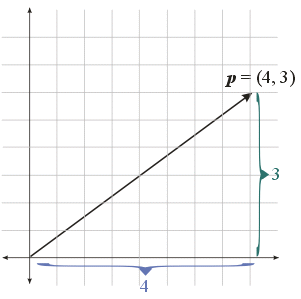
Since the distance from the origin to \(\bs{p}\) is 1, it follows that: \[ \cos(\theta) = \frac{p_1}{1} \\ \sin(\theta) = \frac{p_2}{1} \]
Which is to say that \( \bs{p} := (p_1, p_2) = (\cos(\theta), \sin(\theta)) \)
Hence, any point, \(\bs{q}\), on the unit sphere can be represented as: \[ \bs{q} = (1, 0) \cdot \cos(\theta) + (0, 1) \cdot \sin(\theta) = \bs{i} \cos(\theta) + \bs{j} \sin(\theta) \]
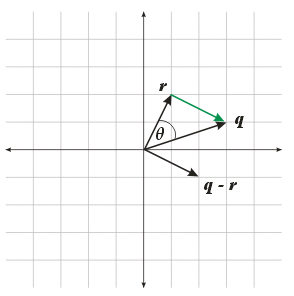
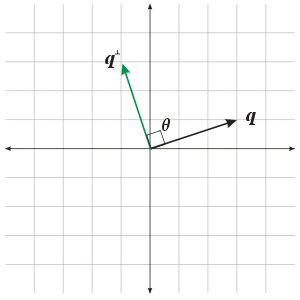
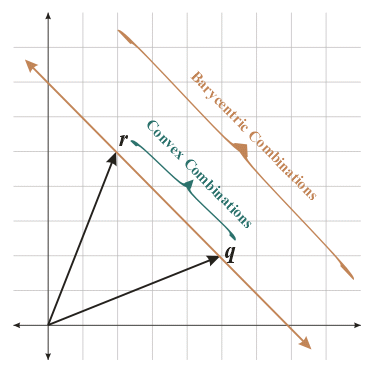
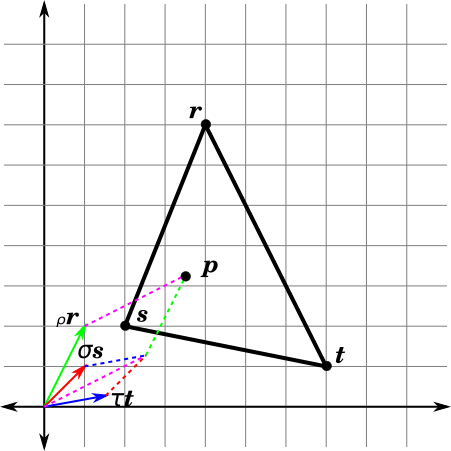
Weighted Combinations of \(\bs{q}\) and \(\bs{r}\)
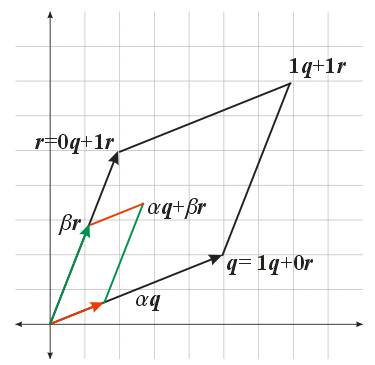
Convex Combinations of \(q\) and \(r\)
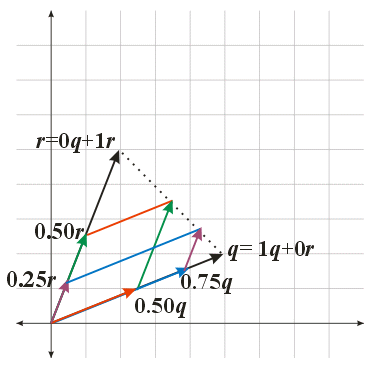
Barycentric Combinations of \(q\) and \(r\)