Triangulation
An Introduction
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
Getting Started
- Surveying:
- Triangulation is the process of determining the location of
a point using angles formed between it and points with known
locations
- Trialateration is the process of determining the location of
a point using the distances between it and points with known
locations
- For Our Purposes:
- We won't distinguish between the two
Using Distances in One Dimension
- The Problem:
- Given one or more points with known locations,
determine the location of a point using the distances
between it and those points
- Notation:
- \(p \in \mathbb{R}\) denotes a point
- \(\cal{C(p, \ell)}\) denotes the set of points
that are exactly distance \(\ell\) from \(p\)
Using Distances in One Dimension (cont.)
- With One Known Location:
- Given the location of the point \(p\) and the
distance from \(p\) to \(a\), determine the
location of the point \(a\)
- A Specific Example:
- \(p\) is located at 4
- The distance from \(p\) to \(a\) is 2
- Visualization:
Using Distances in One Dimension (cont.)
- With One Known Location (cont.):
- You can see from the example that the problem is
under-identified when there is only one known location
- A Specific Example with Two Known Locations:
- \(p\) is located at 4
- The distance from \(p\) to \(a\) is 2
- \(q\) is located at 9
- The distance from \(q\) to \(a\) is 3
- Visualization:
Using Distances in Two Dimensions
- Generalizing the Notation:
- \(p \in \mathbb{R}^2\) now denotes a point
on the plane (i.e., in two dimensions)
- Recall:
- A circle is the set of points in a plane that
are a given distance (called the radius) from
a given point (called the center)
- The Implication:
- We need to find the intersections of circles
Using Distances in Two Dimensions (cont.)
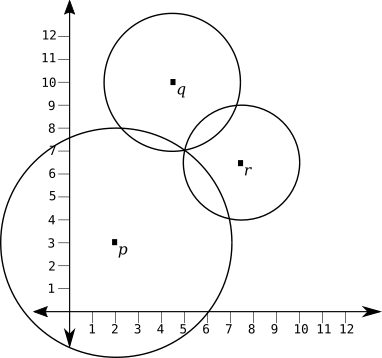
- An Example:
- \(p = (2.0, 3.0)\) and \(\ell(p) = 5.0\)
- \(q = (4.5, 10.0)\) and \(\ell(q) = 3.0\)
- \(r = (7.5, 6.5)\) and \(\ell(r) = 2.5\)
- Visualization:
Using Distances in Two Dimensions (cont.)
- Recall:
- Letting \((h, k)\) denote the center of the circle,
and \(r\) denote its radius, the circle is defined as the
set of points \((x, y)\) that satisfy:
\(
\sqrt{(x - h)^2 + (y - k)^2} = r
\)
- Squaring Both Sides:
-
\(
(x - h)^2 + (y - k)^2 = r^2
\)
Using Distances in Two Dimensions (cont.)
- Intersection of Two Circles:
- They may not intersect
- They may intersect at one point
- They may intersect at two points
- Finding the Intersection:
- Requires a little algebra, but isn't difficult (as long as
you account for the different possibilities)