Route Swapping
An Introduction
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
Motivation
- Review:
- We know how to find "shortest" paths
given travel times/costs/distance
- We understand how congestion impacts travel times/costs
- An Obvious Issue:
- If everyone takes the "shortest" path, it will become
congested and not be the "shortest"
- The Question:
- How might people change their behavior on a
day-to-day basis?
Dynamic vs. Static Models
- Dynamic Models:
- Describes how a system changes over
time (which may be discrete or continuous)
- Static Models:
- Do not explicitly incorporate time
Types of Dynamic Models
- Time-Based Models:
- Describe the system at every point in time regardless of
whether the state of the system changes
- Event-Based Models:
- Describe the system only at times when specific events
(which cause a transition between states) occur
Our Concern
- The Type of Model:
- A time-based (day-to-day) model of route swapping
in response to actual conditions encountered
- An Important Issue:
- Does the model "settle down" over time
Nerd Humor
(Courtesy of xkcd)
"Settling Down"
- Trajectory:
- The state of the system over time
- Steady State:
- A system is in a steady state if the trajectory is unchanging
over time (e.g., a ball that rolls to the bottom of a hill)
- Stability:
- A trajectory is stable if it does not change much under
small perturbations (e.g., a planet in orbit
around the sun)
A Probabilistic Model of Route Swapping
- The Idea:
- People choose the route to use on day \(t+1\)
based only on the route they used on day \(t\)
- They "roll a die" (or use some other random mechanism)
to determine which route to take
- Possible Explanations:
- This is what people are actually doing because they can't
find a pattern in congestion levels
- The modeler doesn't know what the people are actually doing,
but this is consistent with the empirical data
A Probabilistic Example
- Setting:
- People choose between two routes
- Initial Conditions:
- We start with 50 people on each route
A Probabilistic Example (cont.)
- One Set of Probabilities:
- A person on route 1 will switch to route 2 with
probability 1/2 and will stay on route 1 with
probability 1/2
- A person that is on route 2 will switch to route 1 with
probability 1/3 and will stay on route 2 with
probability 2/3
- The Transition Matrix:
- It is convenient to represent the transition probabilities
in a matrix, as follows:
- \(\mathbf{P} = \left[ \begin{array}{c c}
\frac{1}{2} & \frac{1}{2} \\
\frac{1}{3} & \frac{2}{3}
\end{array} \right]
\)
- An Observation:
A Probabilistic Example (cont.)
- After About 10 Days:
- There will be 40 people on route 1 and 60 people on route
2
- From Day 10 On:
- There will be 40 people on route 1 and 60 people on route
2 (i.e., the system will be in steady state)
A Probabilistic Example (cont.)
- A Different Transition Matric:
-
\(\mathbf{P} =
\left[ \begin{array}{l l} 0& 1 \\
1& 0 \end{array} \right]
\)
- What Happens Over Time:
- People bounce back and forth between the two routes
forever
A Deterministic Model of Route Swapping
- The Idea:
- On day \(t+1\), a (fixed) portion of the people switch from
the route they used on day \(t\) to the "best"
route on day \(t\)
- Possible Explanation:
- People get reports about other routes at the end of the
day (from the radio, friends, the WWW, etc.)
- A (fixed) portion are set in their ways
- Notation:
- \(n_i\) denotes the number of vehicles using
route \(i\)
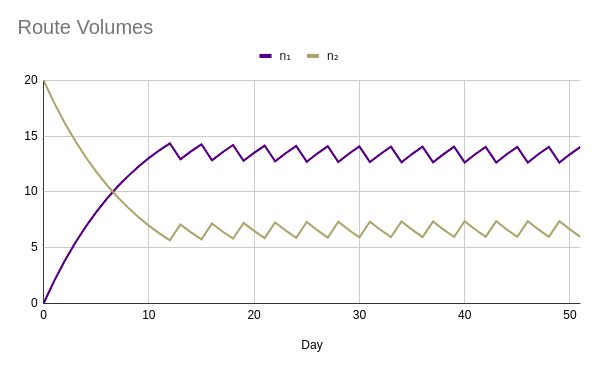
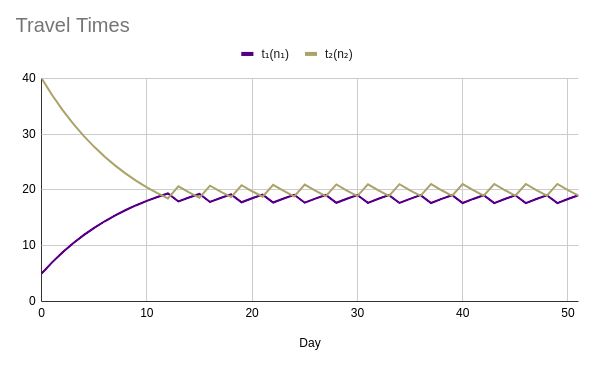
A Deterministic Example
- The Network:
- Two routes connecting one origin-destination pair
- Travel Times/Costs:
- \(t_1(n_1) = 5 + n_1\)
- \(t_2(n_2) = 10 + 1.5 \cdot n_1\)
- Initial Conditions:
A Deterministic Example (cont.)
A Deterministic Example (cont.)
Other Deterministic Models
- State-Dependent Swapping Rates:
- The portion of people that swap depends on the
difference in times/costs
- Multiple Targets:
- People don't just swap to the "best" route, the swap
to all "better" routes