• An Observation:
  • There are many real-world applications in which one needs to find the maximum (or minimum) of a function
• A Reminder:
  • One way to solve such a problem is to take the derivative of the function, set it equal to 0, and solve the resulting equation
• A Difficulty:
  • In many cases this is not possible

• The Chip Monk Chocolate Chip Cookie Company:
  • A local supermarket has agreed to pay you $3.00 per pound for as many pounds of cookies as you can produce
  • The cost of producing cookies varies with the number of cookies you produce
• Some Details:
  • Revenue: \(R(q) = 3q\)
  • Production Cost: \(C(q) = 0.5 q\)
  • Shipping Cost: \(S(q) = 0.0005 q^{2}\)

• Profit:
  • \(\pi(q) = R(q) - C(q) - S(q) = 3.0 q - 0.5 q - 0.005 q^{2} \)
• Maximizing Profit:
  • We could use calculus in this case
  • We want to use a numerical algorithm for illustrative purposes

• Updating the Test Points:
  • Use the golden ratio [\(0.5 (\sqrt{5} - 1)\)]
  • Set \(t_L\) equal to \(L + 0.382 (U - L)\)
  • Set \(t_R\) equal to \(L + 0.618 (U - L)\)
• Why?
  • It's not important
  • Other values between 0.5 and 1 can be used

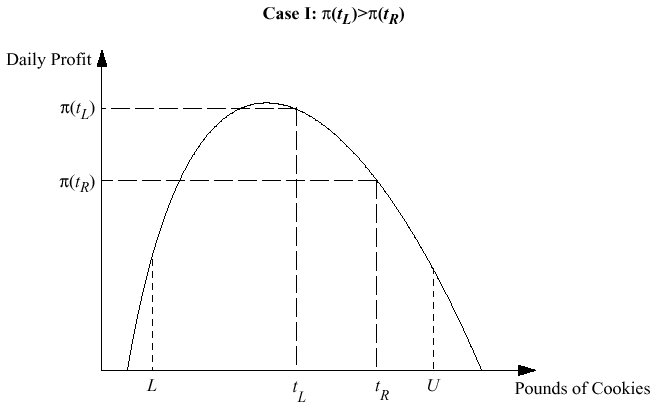
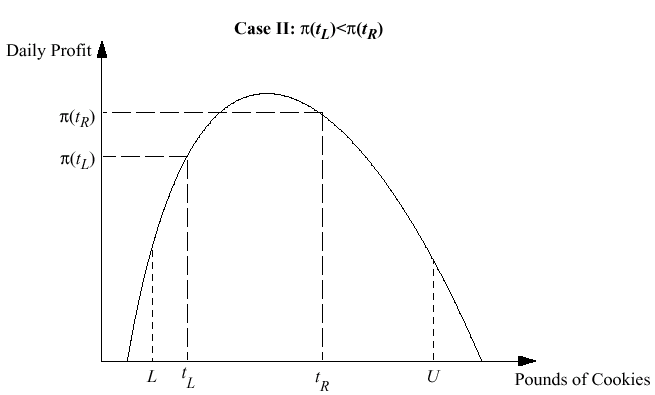
    Choose an initial lower bound L and upper bound U

    Set t_L equal to L + 0.382 * (U - L)
    Set t_R equal to L + 0.618 * (U - L)

    while (U - L is too large} {

      if (The objective function evaluated at t_L is greater
          than the objective function evaluated at t_R) {

            Set U equal to t_R
            Set t_R equal to t_L
            Set t_L equal to L + 0.382 * (U - L)

      } else {

            Set L equal to t_L
            Set t_L equal to t_R
            Set t_R equal to  L + 0.618 * (U - L)
      }
    }
    

cppexamples/optimization/GoldenSection.cpp

        #include "Maximize.h"

/**
 * Maximize a "well-behaved" function using the Golden Section algorithm
 */
double maximize(double (*f)(double), double L_0, double U_0, double tol) {
  double L, t_L, t_R, U;

  // Initialize
  L = L_0;
  U = U_0;

  t_L = L + 0.382 * (U - L);
  t_R = L + 0.618 * (U - L);

  // Iterate
  while ((U - L) > tol) {
    if (f(t_L) > f(t_R)) {
//       L   = L;
      U = t_R;
      t_R = t_L;
      t_L = L + 0.382 * (U - L);
    } else {
      L = t_L;
//       U   = U;
      t_L = t_R;
      t_R = L + 0.618 * (U - L);
    }
  }

  return (U + L) / 2.0;
}