A vector space (also called a linear space) \(P\) over \(\mathbb{R}\) is a non-empty set with the following operations:

Addition: \(\bs{p} + \bs{q} \in P \text{ for each } \bs{p},\bs{q} \in P\)

Multiplication by a Scalar: \(\lambda \bs{p} \in P \text{ for each } \bs{p} \in P, \lambda \in \mathbb{R}\)

which satisfy the following properties:

1. \(\bs{p}+\bs{q} = \bs{q}+\bs{p} \text{ for each } \bs{p},\bs{q} \in P\)
2. \(\bs{p}+(\bs{q}+\bs{r}) = (\bs{q}+\bs{p})+\bs{r} \text{ for each } \bs{p},\bs{q},\bs{r} \in P\)
3. There exists an element \(\bs{0} \in P\) such that \((\bs{p}+\bs{0}) \in P\)
4. For each \(\bs{p} \in P\) there exists an element \(-\bs{p} \in P\) such that \(\bs{p}+(-\bs{p}) = \bs{0}\)
5. \((\lambda+\mu)\bs{p} = \lambda\bs{p} + \mu\bs{p} \text{ for each } \bs{p} \in P, \lambda,\mu \in \mathbb{R}\)
6. \(\lambda(\bs{p}+\bs{q}) = \lambda\bs{p} + \lambda\bs{q} \text{ for each } \bs{p},\bs{q} \in P, \lambda \in \mathbb{R}\)
7. \(\lambda(\mu\bs{p}) = (\lambda\mu)\bs{p} \text{ for each } \bs{p} \in P, \lambda,\mu \in \mathbb{R}\)
8. \(1\bs{p} = \bs{p} \text{ for each } \bs{p} \in P\)

The elements of \(P\) are called vectors.

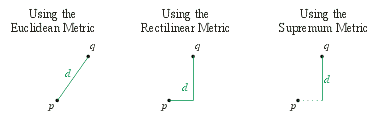
Given a non-empty set of points, \(P\), a metric is a function, \(d\) that assigns a real number to each pair of points (i.e., \(d:P \times P \rightarrow \mathbb{R}\)), satisfying the following properties:

1. \(d(\bs{p}, \bs{q}) \geq 0 \text{ for each } \bs{p},\bs{q} \in P\)
2. \(d(\bs{p}, \bs{q}) = 0 \mbox{ iff } \bs{p} = \bs{q} \text{ for each } \bs{p},\bs{q} \in P\)
3. \(d(\bs{p}, \bs{q}) = d(\bs{q}, \bs{p}) \text{ for each } \bs{p},\bs{q} \in P\)
4. \(d(\bs{p}, \bs{q}) \leq d(\bs{p}, \bs{r}) + d(\bs{q}, \bs{r}) \text{ for each } \bs{p},\bs{q},\bs{r} \in P\) (the triangle inequality)

Given a vector space \(P\) over \(\mathbb{R}\), a norm for \(P\) is a function on \(P\) which assigns to each element a real number (i.e., \(||\cdot||:P \rightarrow \mathbb{R}\)) satisfying the following properties:

1. \(||\bs{p}|| \geq 0 \text{ for each } \bs{p} \in P\)
2. \(||\bs{p}|| = 0 \text{ if and only if } \bs{p} = \bs{0}\)
3. \(||\lambda \bs{p}|| = |\lambda| ||\bs{p} \text{ for each } \bs{p} \in P, \lambda \in \mathbb{R}\)
4. \(||p+q|| \leq ||p|| + ||q|| \text{ for each } \bs{p},\bs{q} \in P\) (the triangle inequality)

Given a vector space, \(P\), and norm, \(||\cdot||\), the function \(d:P \times P \rightarrow \mathbb{R}\) defined by:

\(d(\bs{p},\bs{q}) = ||\bs{p}-\bs{q}||\)

is a metric for \(P\) and is called the metric generated by the norm.

The absolute value function, \(|\cdot|\) is a norm for the set of real numbers, \(\mathbb{R}\).

This norm generates the "usual" metric for \(\mathbb{R}\):

\(d(x,y) = |x-y|\)

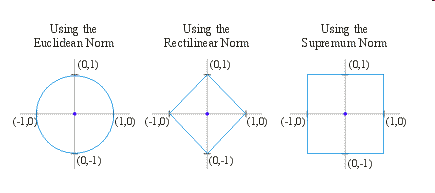
The Euclidean norm is defined on the set of ordered pairs in \(\mathbb{R}^2\) as:

\(||\bs{p}||_2 = \sqrt{p_1^2 + p_2^2}\)

This definition can be extended to the set of ordered \(n\)-tuples in \(\mathbb{R}^n\) as:

\(||\bs{p}||_2 = \sqrt{p_1^2 + p_2^2 + \cdots + p_n^2}\)

To prove that the Euclidean norm generates a metric we need the following result, called the Cauchy-Schwarz inequality.

For any \(\bs{p},\bs{q} \in \mathbb{R}^n\)

\(|\bs{p} \cdot \bs{q}| \leq ||\bs{p}||_2 \cdot ||\bs{q}||_2\)

Proof. For any positive real numbers, \(a,b\), \((a-b)^2 = a^2 - 2ab + b^2 \geq 0\). Hence, \(2ab \leq a^2 + b^2\). Therefore, given non-zero \(\bs{p}\) and \(\bs{q}\), for each \(k\) setting:

\(a = \frac{|p_k|}{\sqrt{\sum_{k=1}^{n}|p_k|^2}}\)

\(b = \frac{|q_k|}{\sqrt{\sum_{k=1}^{n}|q_k|^2}}\)

and summing the resulting inequalities leads to:

\( \frac{\sum_{k=1}^{n}|p_k q_k|} {\sqrt{\sum_{k=1}^{n}|p_k|^2}\sqrt{\sum_{k=1}^{n}|q_k|^2}} \leq 1 \)

The first three properties of a norm are trivial to demonstrate. The triangle inequality can be demonstrated as follows.

\(||\bs{p}+\bs{q}||_2^2 = \left( \sum_{k=1}^{n} |p_k + q_k|^2 \right)\)

\(\leq \sum_{k=1}^{n} |p_k|^2 + 2 \sum_{k=1}^{n} |p_k q_k| + \sum_{k=1}^{n} |q_k|^2\)

So, by the Cauchy-Schwartz inequality:

\(\leq \sum_{k=1}^{n} |p_k|^2 + 2 \sum_{k=1}^{n} |p_k|^2 \sum_{k=1}^{n} |q_k|^2 \sum_{k=1}^{n} |q_k|^2\)

which equals \(\left(||\bs{p}||_2 + ||\bs{q}||)2 \right)^2\).

• The Rectilinear/Manhattan Norm on \(\mathbb{R}^{n}\):
  • \(||\bs{p}||_1 = |p_1| + |p_2| + \cdots + |p_n|\)
• The Supremum (or Uniform) Norm on \(\mathbb{R}^{n}\):
  • \(||\bs{p}||_{\infty} = \max \{|p_1|, |p_2|, \ldots, |p_n| \}\)

For Different Norms

Distance Between Two Points

• The Post Office Metric:
  • \(d_{P}(\bs{p}, \bs{q}) = ||\bs{p}|| + ||\bs{q}|| \mbox{ if } \bs{p} \neq \bs{q}\) (and 0 otherwise)
• The Radar Screen Metric:
  • \(d_{R}(\bs{p}, \bs{q}) = \min \{1, ||\bs{p}-\bs{q}|| \}\)