Map Projections
for a Spherical Planet
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
Motivation
- Some Observations:
- The Earth is not flat
- Maps usually are (especially on computer displays)
- The Implication:
- We need a way to project points on the surface of the
Earth onto a map
Thinking About Map Projections
- Using a Physical Model:
- Algebraically:
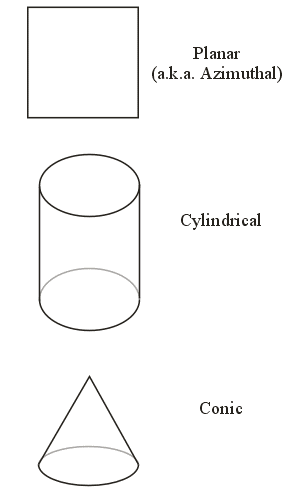
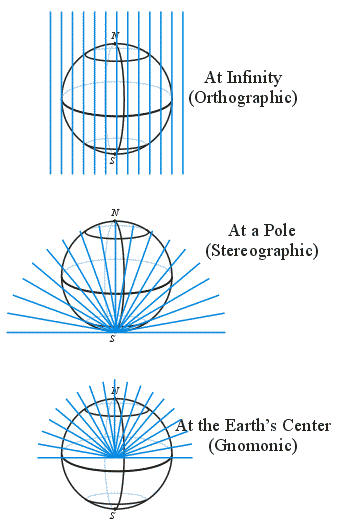
Physical Models
- The Idea:
- Shine a light onto or through a transparent Earth
and capture the shadows cast by the opaque features
- The "Parameters":
- The shape of the screen (called the projection surface)
- The position of the projection surface
- The location of the light source
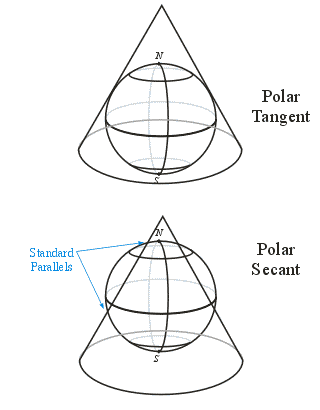
Positioning a Planar Projection Surface
Positioning a Cylindrical Projection Surface
Positioning a Conical Projection Surface
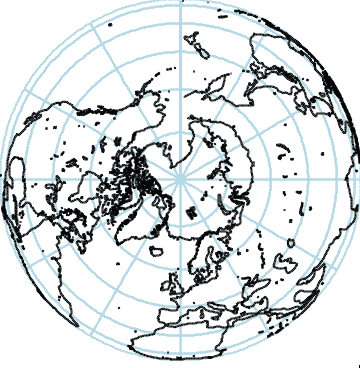
Polar Azimuthal Orthographic Projection
Notation
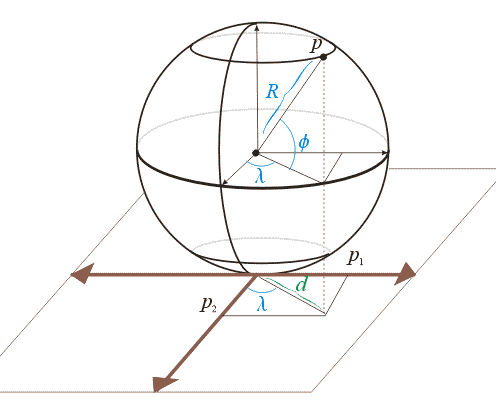
Polar Azimuthal Orthographic Projection (cont.)
- Derivation of the Projection:
- \(\cos \phi = d / R \Rightarrow d = R \cos \phi\)
- \(\cos \lambda = p_{2}/d \Rightarrow p_{2} = d \cos \lambda
= R\cos \phi \cos \lambda\)
- \(\sin \lambda = p_{1}/d \Rightarrow p_{1} = d \sin \lambda
= R \cos \phi \sin \lambda\)
- \(\)
- Derivation of the Inverse:
- \(d = ||\bs{p}||\)
- \(\cos \lambda = \frac{p_{2}}{||\bs{p}||} \Rightarrow
\lambda = \cos^{-1}(\frac{p_{2}}{||\bs{p}||})\)
- \(\cos \phi = d / R \Rightarrow
\phi = \cos^{-1}(\frac{||\bs{p}||}{R})\)
Polar Azimuthal Orthographic Projection (cont.)
The World
Cylindrical Stereographic Projection
Notation
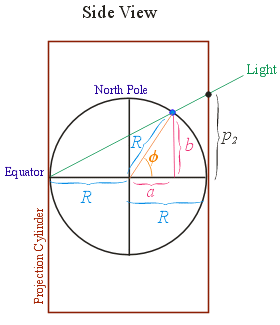
Cylindrical Stereographic Projection (cont.)
- Derivation of the Projection:
- Since the triangles are "similar" \(\frac{b}{R+a} = \frac{p_{2}}{R+R}\), hence \(p_{2} = (\frac{b}{a+R})2R\)
- \(\sin \phi = b/R \Rightarrow b = R \sin \phi\)
- \(\cos \phi = a/R \Rightarrow a = R \cos \phi\)
- So, \(p_{2} = \frac{R \sin \phi}{R+R\cos \phi}2R=\frac{R \sin \phi}{R(1+\cos \phi)}2R = \frac{\sin\phi}{1+\cos\phi}2R\)
- \(p_{1} = \lambda R\) since it is only determined by
where the cylinder is "cut"
- Derivation of the Inverse:
- \(\lambda = p_{1}/R\)
- \(\tan \phi = p_{2}/R \Rightarrow
\phi = \tan^{-1}(p_{2}/R)\) (but you have to be careful
about the domain of the \(\tan\))
Desirable Properties of Projections
- The Most Common:
- Conformal (i.e., angles are preserved)
- Equal Area (i.e., areas are in constant proportion)
- Equidistant (i.e., distances are in constant proportion)
- An Important Mathematical Result:
- A single projection can not be both conformal
and equal area
Desirable Properties of Projections (cont.)
Nerd Humor - Bad Map Projection: South America
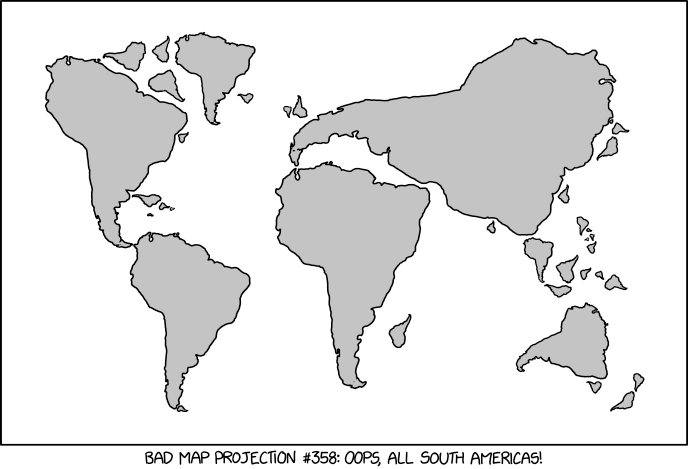
(Courtesy of xkcd)
Sinusoidal Projection
- Derivation of an Equal Area Projection:
- Uniformly space the parallels so \(p_{2} = \phi R\)
- To be equal area given these parallels, the length of
each parallel has to equal the "circumference" at that
latitude (which is \(R \cos \phi\))
- The projected parallel must be proportional to this
circumference so it must have length \(k 2 \pi R \cos
\phi\)
- To be consistent at the equator (where the "circumference"
is \(2 \pi R\)), we must have \(k = 0.5\)
- Assuming a constant horizontal scale, we must have
\(\frac{p_{1}}{\pi R \cos \phi} = \frac{\lambda}{\phi}\)
- So, \(p_{1} = \lambda R \cos \phi\)
- Note:
- We did not use a physical model
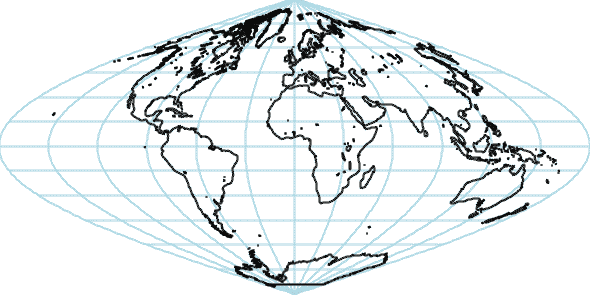
Sinusoidal Projection (cont.)
The World
Equatorial Cylindrical Equal Area Projection
- Parameters:
- \(\lambda_{0}\) is the standard longitude
(i.e., the horizontal center of the projection)
- Projection:
- \(p_{1} = R (\lambda - \lambda_{0}) \)
- \(p_{2} = R \sin(\phi)\)
- Inverse:
- \(\lambda = \lambda_{0} + \frac{p_{1}}{R}\)
- \(\phi = \sin^{-1}(p_{2} / R)\)
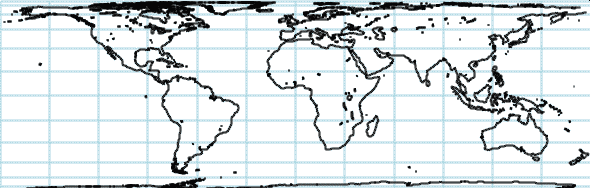
Equatorial Cylindrical Equal Area Projection (cont.)
The World
Equatorial Cylindrical Conformal Projection (Mercator)
- Parameters:
- \(\lambda_{0}\) is the standard longitude
- Projection:
- \(p_{1} = R (\lambda - \lambda_{0}) \)
- \(p_{2} = R \ln[\tan(\pi / 4 + \phi / 2)]\)
- Inverse:
- \(\lambda = \lambda_{0} + \frac{p_{1}}{R}\)
- \(\phi = 2 [\tan^{-1}(e^{\frac{p_{2}}{R}}) - \pi / 4]\)
Equatorial Cylindrical Conformal Projection (cont.)
The World
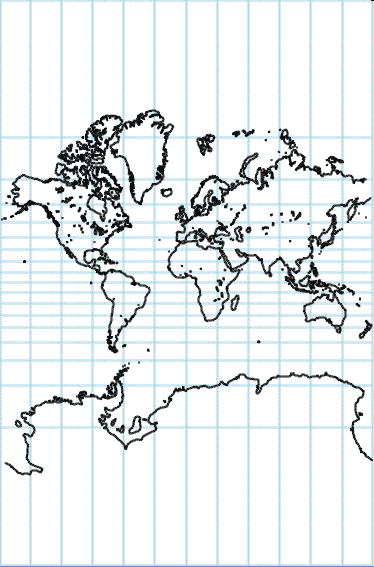
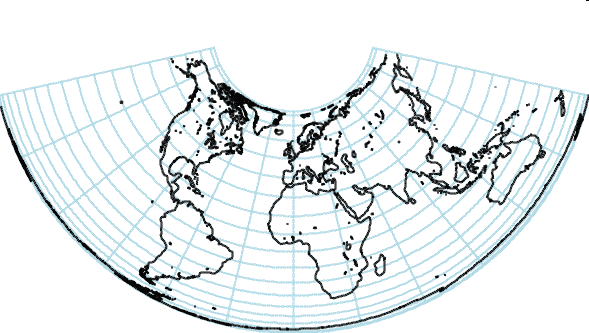
Conical Equal Area Projection (Albers)
- Parameters:
- \(\lambda_{0}\) and \(\phi_{0}\) are the longitude and latitude of the origin of the transformed coordinates
- \(\phi_{1}\) and \(\phi_{2}\) are
the two standard parallels (i.e., the parallels where the
cone intersects the sphere)
- Preliminary Calculations:
- \(n = 0.5 (\sin(\phi_{1}) + \sin(\phi_{2}))\)
- \(c = \cos^{2}(\phi_{1}) + 2 n \sin(\phi_{1})\)
- \(\rho_{0} = \frac{\sqrt(c - 2 n \sin(\phi_{0}))}{n}\)
- Projection:
- \(\rho = \frac{\sqrt{c - 2 n \sin(\phi)}}{n}\)
- \(\theta = n(\lambda - \lambda_{0}) \)
- \(p_{1} = R \rho \sin(\theta)\)
- \(p_{2} = R (\rho_{0} - \rho \cos(\theta))\)
- Inverse:
- \(a = \sqrt{(p_{1}/R)^{2}+(\rho_{0}-p_{2}/R)^{2}}\)
- \(b = \tan^{-1}((p_{1}/R)/(\rho_{0} - p_{2}/R))\)
- \(\phi = \sin^{-1}(\frac{c- a^{2} n^{2}}{2n})\)
- \(\lambda = \lambda_{0} + b/n\)
Conical Equal Area Projection (cont.)
The World