Map Matching
An Introduction
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
The Map-Matching Problem
- The Situation:
- A person/vehicle is moving along a finite set
of streets \(\overline{\mathcal{N}}\)
- We are provided with an estimate of this person's
location at a finite number of points in time
denoted \(\{0, 1, ..., T \}\)
- The person's actual location at time \(t\)
is denoted by \(\overline{P}^{t}\) and the
estimate is denoted by \(P^{t}\)
- The Problem:
- Find the street in \(\overline{\mathcal{N}}\)
that contains \(\overline{P}^{t}\)
The Map-Matching Problem (cont.)
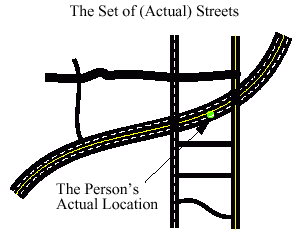
- A Complication:
- We do not know the street system,
\(\overline{\mathcal{N}}\) exactly
- We have a
network (or graph)
representation \(\mathcal{N}\) and a set of piecewise linear
curves (one curve associated with each arc/link)
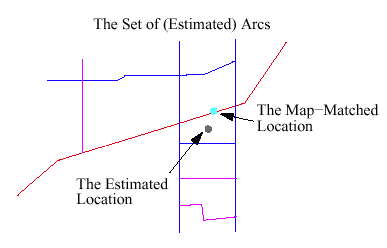
- The Actual Problem(s):
- Match the estimated location \(P^{t}\) with a
curve, \(A\) in the "map"
- Then determine the street
\(\overline{\mathcal{A}} \in \overline{\mathcal{N}}\) that
corresponds to the actual location \(\overline{P}^{t}\)
- A secondary concern is to determine the position on the
curve \(A\) that best corresponds to
\(\overline{P}^{t}\)
The Map-Matching Problem (cont.)
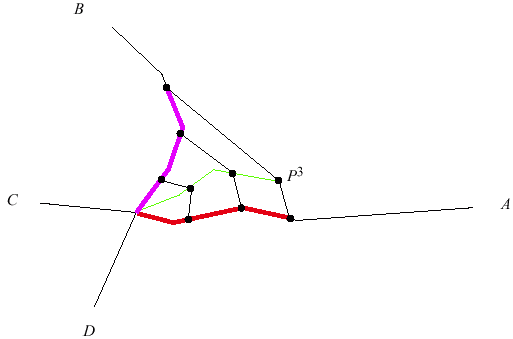
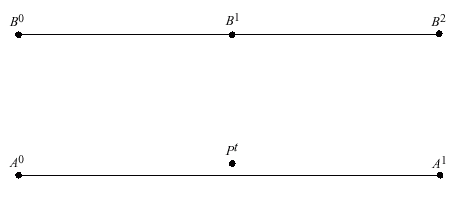
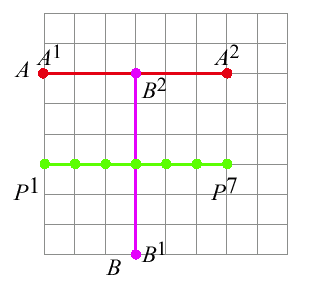
Point-to-Point Matching
- The Idea:
- Match Pt
to the "closest"
breakpoint in the piecewise linear curve
- A Difficulty:
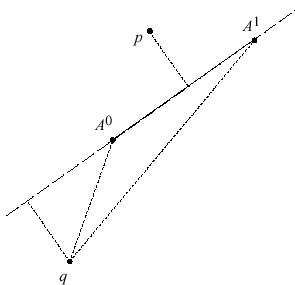
Point-to-Curve Matching
- The Idea:
- Identify the arc that is closest to
\(P^{t}\)
- One Approach:
Point-to-Curve Matching (cont.)
Point-to-Curve Matching (cont.)
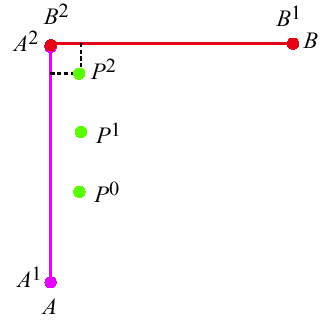
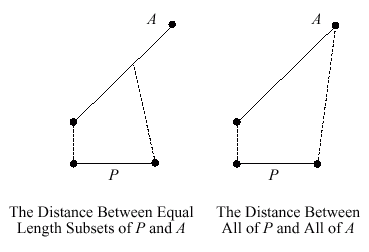
Curve-to-Curve Matching
- The Idea:
- Find the arc that is closest to the piecewise
linear curve, \(P\)
defined by the points
\(P^{0}, P^{1}, ..., P^{m}\)
- A Difficulty:
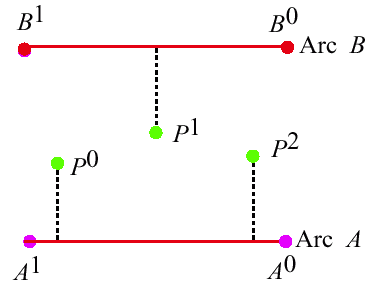
Curve-to-Curve Matching (cont.)
- Another Approach:
- A Difficulty:
Curve-to-Curve Matching (cont.)
- Another Approach:
- "Correct" for differences in length
- A Difficulty:
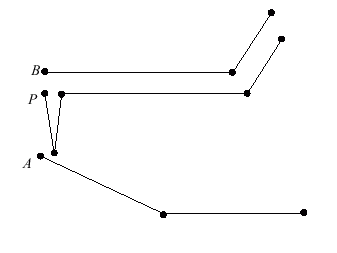
Using Topological Information
Getting Started
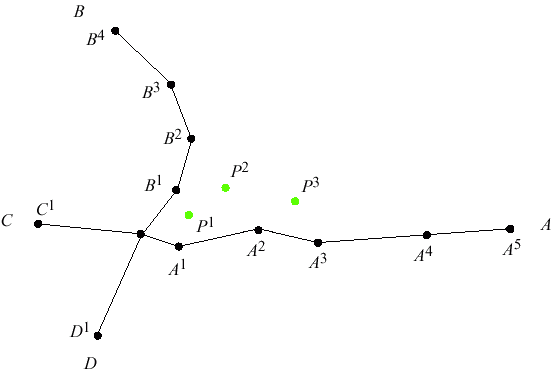
Using Topology (cont.)
Using Connectivity/Topology