• Object Space:
  • Work object-by-object
• Image Space:
  • Work pixel-by-pixel

• This is a Well-Studied Problem:
  • Hundreds of algorithms have been developed
  • They tend to be special-purpose (e.g., fast, realistic)
• We'll Consider Two Representative Algorithms:
  • Object Space: Binary Space Partitioning
  • Image Space: Z-Buffer

• Approach:
  1. Order objects from back to front
  2. Render from back to front (sometimes called a "Painter's Algorithm")
• Schumacker's Algorithm (1969):
  • Works with convex polygons (which can be separated by a plane)
• The Algorithm Presented Here:
  • Works with triangles

• A Simple Case:
  • Partition points on a plane relative to a front edge
• Visualization:
  • 

• An Observation:
  • One point is either to the front of or the back of another point
• Using a Binary Tree:
  • We can represent the relationship between points using a binary tree in which each node has a back branch and a front branch

Building the Tree

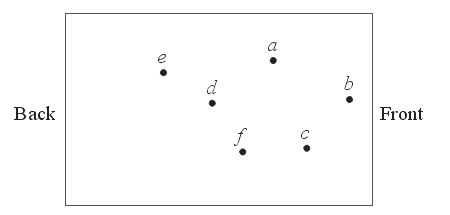
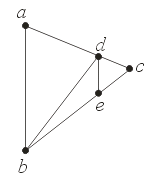
  root = new Node(point[0])

  for (i = 1...N-1) {
    add(point[i], root)
  }
  

  add(Point p, Node n) {
    if (p inFrontOf n.point) {
        if (n.front == null) n.front = new Node(p)
        else                 add(p, n.front) 
    } else {
        if (n.back == null)  n.back = new Node(p)
        else                 add(p, n.back) 
    }
  }
  

• The Example Revisited:
  • 
• Building the Tree:
  • 

Rendering using In-Order Tree Traversal

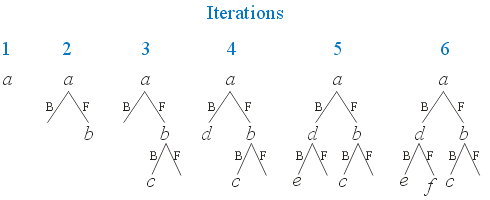
    inOrder(Node current) {
        if (current != null) {
            inOrder(current.front)

	    render(current.p)

	    inOrder(current.back)
        }
    }
    

• Triangles in 2D:
  • We can partition based on whether one triangle will "hide" another
  • This leads to a partial ordering (sometimes called a \(z\text{-order}\)
• A Big Difference of 3D:
  • We can't always order the triangles
  • 

• Comparing Triangles:
  • Given a triangle, \(T\), we want to know whether the viewer, \(v\), is on the same side of the plane containing \(T\) as another triangle, \(S\)
• Visualization:
  • 

• Recall:
  • A triangle with vertices \(\bs{a}\), \(\bs{b}\), and \(\bs{c}\) defines a plane
  • The (non-unit) normal vector for that triangle is given by \((\bs{b} - \bs{a}) \times (\bs{c} - \bs{a})\)
  • A plane creates two halfspaces, identifiable by the sign of \(\bs{n} \cdot (\bs{p} - \bs{x})\) where \(\bs{x}\) is any point on the plane
• Comparing \(S\) and \(\bs{v}\):
  • Find the sign of \(\bs{n} \cdot (\bs{v} - \bs{a})\)
  • Find the sign of \(\bs{n} \cdot (\bs{p} - \bs{a})\) for each vertex, \(\bs{p}\) of \(S\)

• The Easy Case:
  • All vertices of \(S\) are on the same side of the plane
• A More Difficult Case:
  • 

• Handling the More Difficult Case:
  • Split the triangle (which means, since we are working only with triangles, that we must split it into three triangles)
• Visualization:
  • 

• Approach:
  • Work with the shapes after they have been projected
  • Only render a pixel if it is in front of whatever was previously rendered there
• Where the Algorithms get their Name:
  • Use a buffer the same size as the frame buffer to keep track of the front-most \(z\)-value at each pixel

• Recall:
  • In scan line filling you find the intersection of each row in the frame buffer and the edges of the triangle
  • You then fill each pixel between the two intersections
• Visualization:
  • 

• Important:
  • You need to keep the original \(z\)-values when "projecting" (i.e., don't actually project onto the plane \(z=0\))
• Pre-Processing for Each Scan Line:
  • When finding the intersection of the scan line with the edges, make sure the intersection is within the segment
  • Use the \(x\) coordinate of the intersection (which must be calculated) to determine whether an edge is the left edge or the right edge
  • Calculate the \(z\) coordinate of the intersection
• For Each Point/Pixel on the Scan Line:
  1. Interpolate the \(z\) value for the point/pixel \(z\) values for the left and right intersections
  2. Check the \(z\) value of the point with the value in the \(z\)-buffer
  3. Update the value in the \(z\)-buffer if necessary

• Running Time:
  • Very little extra work is needed over and above 2D scan line rendering
• Space Requirements:
  1. We need a \(z\)-buffer with the same dimensions as the frame buffer
  2. The size of each element in the \(z\)-buffer depends in the number of possible "depths"

• An Example:
  • 
• Two Points on the Scan Line:
  • \(\bs{g} = [0 \;\; 3]\)
  • \(\bs{h} = [9 \;\; 3]\)
• Parametric Forms in 2D:
  • The "From" Edge: \(\mathcal{F}(\phi) = \bs{a} + \phi (\bs{c} - \bs{a})\)
  • The "To" Edge: \(\mathcal{T}(\tau) = \bs{b} + \tau (\bs{c} - \bs{a})\)
  • The Scan Line: \(\mathcal{S}(\sigma) = \bs{g} + \sigma (\bs{h} - \bs{g})\)

• Finding the Intersection of \(L\) and \(S\):
  • \(\phi = \frac{(\bs{g} - \bs{a}) \cdot (\bs{h} - \bs{g})^{\perp}} {(\bs{c} - \bs{a}) \cdot (\bs{h} - \bs{g})^{\perp}} = \frac{[-5 \; \; -6]^T \cdot [0 \; \; -9]^T} {[-4 \; \;-8]^T \cdot [0 \; \; -9]^T} = \frac{-54}{-72} = 0.750\) (which is in \([0, 1]\))
  • \(\sigma = \frac{(\bs{a} - \bs{g}) \cdot (\bs{c} - \bs{a})^{\perp}} {(\bs{h} - \bs{g}) \cdot (\bs{c} - \bs{a})^{\perp}} = \frac{[5 \; \; 6]^T \cdot [8 \; \; -4]^T} {[9 \; \; 0]^T \cdot [8 \; \; -4]^T} = \frac{16}{72} = 0.222\) (which is in \([0, 1]\))
• Finding the Intersection of \(M\) and \(S\):
  • \(\tau = \frac{(\bs{g} - \bs{b}) \cdot (\bs{h} - \bs{g})^{\perp}} {(\bs{c} - \bs{a}) \cdot (\bs{h} - \bs{g})^{\perp}} = 0.500\) (which is in \([0, 1]\))
  • \(\sigma = \frac{(\bs{b} - \bs{g}) \cdot (\bs{c} - \bs{a})^{\perp}} {(\bs{h} - \bs{g}) \cdot (\bs{c} - \bs{a})^{\perp}} = 0.556\) (which is in \([0, 1]\))
• Visualization:
  • 

• The Triangle (with the \(z\)-Coordinates):
  • \(\bs{a} = [5 \;\; 9 \;\; 20]^T\)
  • \(\bs{b} = [9 \;\; 5 \;\; 20]^T\)
  • \(\bs{c} = [1 \;\; 1 \;\; 10]^T\)
• \(z\) at the Intersections with the Scan Line:
  • Pixel \((2,3)\): We know that this point is given by \(0.75\bs{c} + 0.25\bs{a}\). Expanding yields

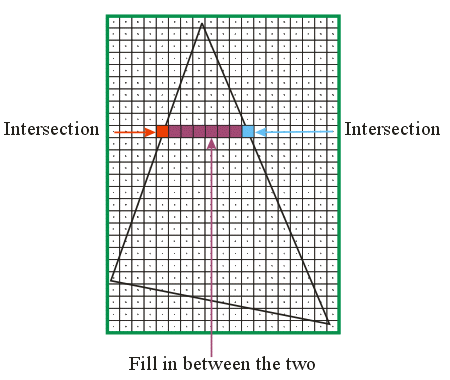
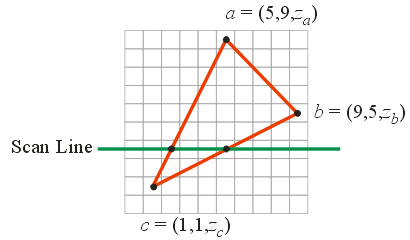
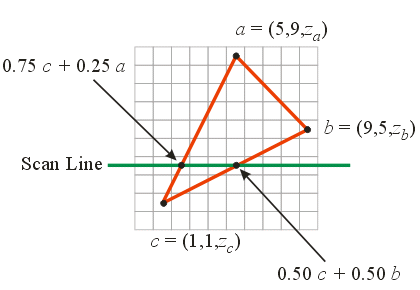
    \(0.75 [1 \;\; 1 \;\; 10]^T + 0.25 [5 \;\; 9 \;\; 20]^T =\)
    \([0.75 \;\; 0.75 \;\; 7.50]^T + [1.25 \;\; 2.25 \;\; 5.0]^T =\)
    \([2.00 \;\; 3.00 \;\; 12.50]^T\)

    which has a \(z\)-coordinate of \(12.50\) (and the correct \(x\)-coordinate and \(y\)-coordinate)
  • Pixel \((5,3)\): We know that this point is given by \(0.50\bs{c} + 0.50\bs{b}\). Expanding yields

    \(0.50 [1 \;\; 1 \;\; 10]^T + 0.50 [9 \;\; 5 \;\; 20]^T =\)
    \([0.50 \;\; 0.50 \;\; 5.00]^T + [4.50 \;\; 2.50 \;\; 10.0]^T =\)
    \([5.00 \;\; 3.00 \;\; 15.00]^T\)

    which has a \(z\)-coordinate of \(15.00\) (and the correct \(x\)-coordinate and \(y\)-coordinate)

• Moving Along the Scan Line:
  • We need to interpolate horizontally between \((2,3)\) and \((5,3)\)
• Calculating the Interpolation Parameter \(\pi\) for a Pixel:
  • We move from \((2,3)\) to \((5,3)\) (which has a length of 3), one pixel at a time
  • \(\pi\) is the proportion of the length that has been "traveled" to get to that pixel (e.g., 1 out of a total of 3 for pixel \((3,3)\))
• \(\pi\) for Each Pixel:
  • Pixel \((2,3)\): \(\pi = \frac{2 - 2}{5 - 2} = \frac{0}{3}\)
  • Pixel \((3,3)\): \(\pi = \frac{3 - 2}{5 - 2} = \frac{1}{3}\)
  • Pixel \((4,3)\): \(\pi = \frac{4 - 2}{5 - 2} = \frac{2}{3}\)
  • Pixel \((5,3)\): \(\pi = \frac{5 - 2}{5 - 2} = \frac{3}{3}\)

• Interpolating Along the Scan Line:
  • The pixel is given by \( (1 - \pi) [2.00 \;\; 3.00 \;\; 12.50]^T + \pi [5.00 \;\; 3.00 \;\; 15.00]^T\)
• Performing the Calculations:
  • Pixel \((3,3)\): \( \frac{2}{3} [2.00 \;\; 3.00 \;\; 12.50]^T + \frac{1}{3} [5.00 \;\; 3.00 \;\; 15.00]^T = [3.00 \;\; 3.00 \;\; 13.33]^T\)
  • Pixel \((4,3)\): \( \frac{1}{3} [2.00 \;\; 3.00 \;\; 12.50]^T + \frac{2}{3} [5.00 \;\; 3.00 \;\; 15.00]^T = [4.00 \;\; 3.00 \;\; 14.17]^T\)

• Comparing \(z\)-Values:
  • At each pixel, compare the calculated \(z\)-coordinate with the value in the \(z\)-buffer
• Using the Comparison:
  • If the \(z\)-coordinate is closer to the viewer then change the color of the pixel in the frame buffer (based on the color of the pixel obtained using the lighting model)

• Floating Horizon Algorithms:
  • Used for parametric surfaces
• Roberts' Algorithm and Related:
  • Object space algorithms
• Warnock's Algorithm and Related:
  • Object space algorithms that use quadtrees