• An Observation About Arrays:
  • Elements in an array must be "identified" using an int index
• One Example:
  • A (homogenous) collection of university students
  • Each student has a complicated ID number (like a Social Security Number) that either can't or shouldn't be represented as an int and aren't sequential
• Another Example:
  • A (homogeneous) collection of houses in a single city/town
  • Each house has a unique address that can be used to identify it, but this address is not an int

• Design an ADT that has array-like operations but can use an index of any type
• Consider the efficiency of different implementations of this ADT

Map

Values:	Homogeneous elements of any type
Operations:	Name/Operator Arguments Returns Constructor A new instance. put key The key/index of the element to add/insert value The value of the element to add/insert get key The key/index of the element to retrieve The value of the element with the given key/index

In addition, one could add an isEmpty() operation, an isFull() operation (if there is a size limit), a remove() operation, and a makeEmpty() operation.

• Motivation:
  • One obvious way to proceed is to simply convert the non-integer index (which we will call a key), into an integer index and then use an array
• Definitions:
  • The process of converting a key into an integer is called hashing
  • A function that performs this operation is called a hash function

An Example: We need to "index" a collection of books written by Sue Grafton because we are developing an "instant printing" service that charges by the page

Title	Pages
A Is for Alibi	214
B Is for Burglar	211
C Is for Corpse	212
D Is for Deadbeat	239
E Is for Evidence	199
F Is for Fugitive	308
G Is for Gumshoe	341
H Is for Homicide	287
I Is for Innocent	343
J Is for Judgment	376
K Is for Killer	307
L Is for Lawless	322
M Is for Malice	337
N Is for Noose	322
O Is for Outlaw	318

We would like a hash function that converts each of these titles into a unique integer in the closed interval [0, 15]. One such function is:

    int graftonHash(char *key)
    {
      int result;

      result = key[0] - 'A';
      return result;
    }
   

General Minimal Perfect Hash Functions

Cichelli, R.J. (1980) "Minimal Perfect Hash Functions Made Simple", Communications of the ACM, Vol. 23, pp. 17-19.

Czech, Z.J. and Majewski, B.S. (1993) "A Linear Time Algorithm for Finding Minimal Perfect Hash Functions", Computer Journal, Vol. 36, pp. 579-587.

Fox, E.A., Heath, L.S., Lenwood, S., Chen, Q.F. and Daoud, A.M. (1992) Practical Minimal Perfect Hash Functions for Large Databases, Communications of the ACM, Vol. 35, pp. 105-121.

Haggard, G. and Karplus, K. (1986) "Finding Minimal Perfect Hash Functions", SIGCSE Bulletin, Vol. 18, pp. 191-193.

An Example: We have a collection of holidays and we want to "index them" by date (where each date is in the form MMDD). We could use MM*100 + DD but...

    // Hash a date into the closed interval [0, 365]
    int hashDate(char *mm, char *dd)
    {
      int   d, result, m;
      int   days[12] = {0,31,60,91,121,152,182,213,244,274,305,335};


      m = atoi(mm);   // Convert a string to an int
      d = atoi(dd);

      result = days[m-1] + d;
      return result;
    }
    

The Date Example (cont.)

    int hashDate2(char *mm, char *dd)
    {
      int   d, result, m;


      m = atoi(mm);   // Convert a string to an int
      d = atoi(dd);

      result = d * m - 1;
      return result;
    }
    

This is an imperfect hash function because more than one key can generate the same integer. For example, March 10 hashes to 29. and October 3 also hashes to 29.

• An Observation:
  • In many cases it is difficult, or impractical, to develop a perfect hash function
• Imperfect Hash Functions:
  • Convert the key into an integer (often using the ASCII values of the characters)
  • Reduce the range

• Mid-Square Technique:
  • The numeric key is squared
  • The central digits are adjusted to fit into the range
• An Example:
  • The 6-digit key 172148 needs to hash into the interval [0,7000)
  • The key is squared to yield 029634933904
  • The middle four digits are selected (i.e., 3493)
  • To ensure that the hashed integer is in [0,7000) this number is multiplied by 7 and divided by 10 to yield 2445

• The Division Technique:
  • The key is divided into the upper limit of the range and the remainder is used
  • More formally, letting \(k\) denote the key and \(s-1\) denote the largest index desired, the function used is \(k % s\)
• The Same Example:
  • \(172148 % 7000 = 4148\)

• The Radix Technique:
  • The number is treated as if it has a different base, excess high-order digits are dropped, and the number is scaled
• The Same Example:
  • Using the key 172148 and base 11 we have \(1 \cdot 11^5 + 7 \cdot 11^4 + 2 \cdot 11^3 + 1 \cdot 11^2 + 4 \cdot 11^1 + 8 \cdot 11^ 0 = 266373\)
  • The 4 low-order digits are 6373
  • This can be multiplied by 7 and divided by 10 to yield 4461
  • (Note that this particualr conversion can be performed efficiently using a series of shifts and additions.)

The ELFhash (Used by the UNIX Executable and Linking Format)

    unsigned long ELFhash(const char *key) {

      unsigned long  h, g;

      while (*key) {

        h = (h << 4) + *key++;
        if (g = h & 0xF0000000) h ^= g >> 24; // This is = not ==

        h &= ~g; // This is sometimes incorrectly listed as h&=g
      }

      return h;
    }
   

where & is the bitwise logical AND operator, ^ is the bitwise XOR opertor, ~ is the bitwise NOT operator, >> is the shift right operator, and << is the shift left operator.

• Using a Perfect Minimal Hash Function:
  • The elements in the hashmap can be stored in an array
• Using a Perfect Hash Function:
  • One can still use an array to hold the elements of the hashmap
  • The only difficulty is that some space will be wasted

• Using an Imperfect Hash Function:
  • Two keys can hash to the same integer (which is referred to as a collision)
• An Example:
  • Returning to the holiday example, both March 10 and October 3 hash to the same integer (i.e., 29)
  • Only one of these dates can use element 29 of the array
  • The other must be stored someplace else
• Resolving Collisions:
  • Linear Probing
  • Chaining
  • Rehashing
  • Quadratic Probing
  • Random Probing

• The Algorithm:
  • Search until we find an available slot
  • If slot \(H(k)\) is unoccupied, \(k\) is not in the map. If \(H(k)\) is occupied the map is searched in a circle (which can be accomplished using the % operator) until an empty slot is found
• An Example:
  • Start by inserting \(A_5\), \(A_2\) and \(A_3\) (where the subscript denotes the hashed integer of the key):
    

    \(A_2\)

    \(A_3\)

    \(A_5\)

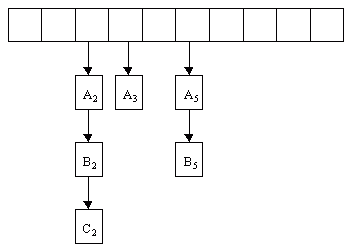
  • Next, let's insert \(B_5\). Since slot 5 is not empty, we perform a linear search until an empty slot is found:
    

    \(A_2\)

    \(A_3\)

    \(A_5\)

    \(B_5\)

  • Next, let's insert \(B_2\). Since slot 2 is not empty, we perform a linear search until an empty slot is found:
    

    \(A_2\)

    \(A_3\)

    \(B_2\)

    \(A_5\)

    \(B_5\)

  • Finally, let's insert \(C_2\). Since slot 2 is not empty, we perform a linear search until an empty slot is found:

    \(A_2\)

    \(A_3\)

    \(B_2\)

    \(A_5\)

    \(B_5\)

    \(C_2\)

• The Algorithm:
  • The elements in the map are not stored in an array
  • Instead, the array contains pointers to linked structures and collisions are resolved by expanding the appropriate linked structure
  • This is called an open hashmap
• An Illustration:
  • 

• Multiple hash functions, \(H_1(k), H_2(k), ...H_m(k)\), are used
• If a collision occurs with \(H_i(k)\) then \(H_{i+1}(k)\) is used, etc...

• One Important Implication:
  • Can't use a closed hashmap (i.e., the elements can't be stored in an array)
• An Alternative:
  • Use an open hashmap

• A Definition:
  • A hashmap with \(n\) slots and \(m\) entries has a load factor of \(a=m/n\)
• An Important Observation:
  • The performance of a hashmap depends on the load factor
• Some Details:
  • When \(a\) is small, many "searches" will require only 1 "operation"
  • When \(a\) is large, many "searches" will require only \(n\) "operations"
  • Assuming that the distribution of hashes is uniform it is possible to derive the "expected" number of probes for successful and unsuccesful searches (see the textbook for a summary)

Typical Results

	Linear Probing		Double Hashing
\(a\)	Successful	Unsuccessful	Successful	Unsuccessful
0.10	1.1	1.1	1.1	1.1
0.20	1.1	1.3	1.1	1.2
0.30	1.2	1.5	1.2	1.4
0.40	1.3	1.9	1.3	1.7
0.50	1.5	2.5	1.4	2.0
0.60	1.8	3.6	1.5	2.5
0.70	2.2	6.1	1.7	3.3
0.80	3.0	13.0	2.0	5.0
0.90	5.5	50.5	2.6	10.0

• A Common Belief:
  • Many people argue that you can avoid collisions by making the size a prime number
• Closest Prime Numbers:

  Number	Closest Prime
  100	97
  250	241
  500	499
  1000	997
  1500	1499
  2000	1999
  5000	4999
  7500	7499
  10000	9973