|
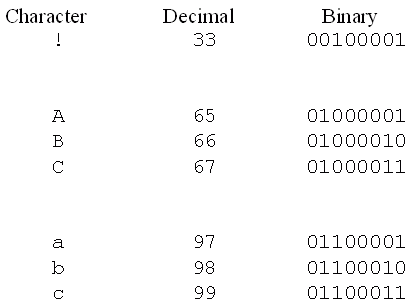
The Representation of Data
An Overview |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
|
The Representation of Data
An Overview |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
What Is This?


 : Negative Numbers (cont.)
: Negative Numbers (cont.)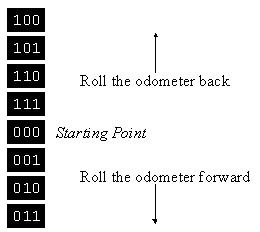
 : Negative Numbers (cont.)
: Negative Numbers (cont.)
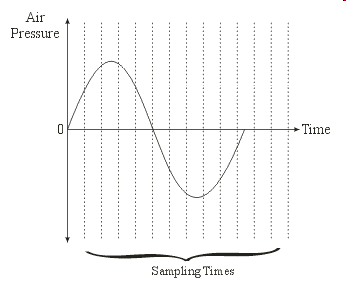
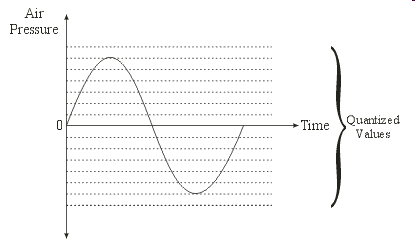
 : What About Real Numbers? (cont.)
: What About Real Numbers? (cont.) : What About Real Numbers? (cont.)
: What About Real Numbers? (cont.)