|
Critical Path Methods
An Introduction |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
|
Critical Path Methods
An Introduction |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
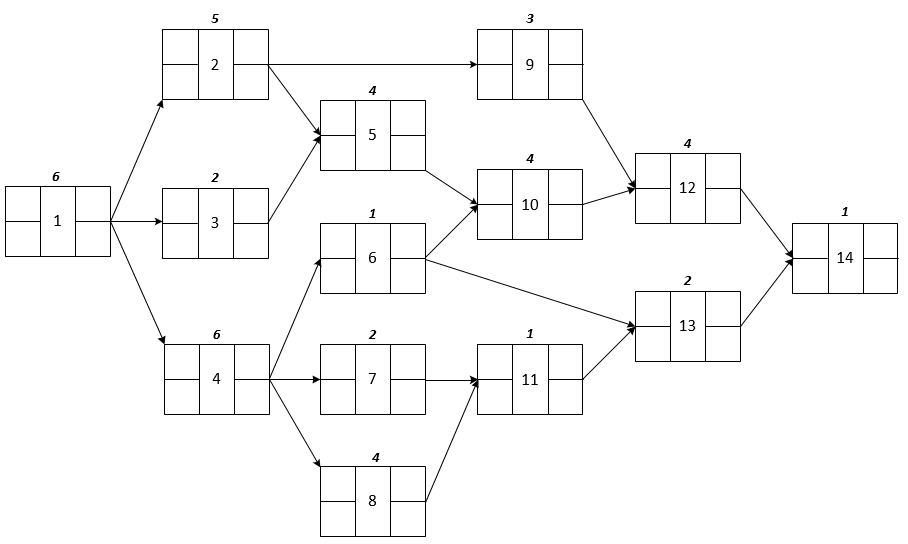
The Input Data
Getting Started
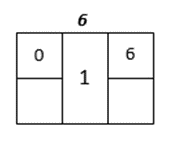
Adding Dependencies
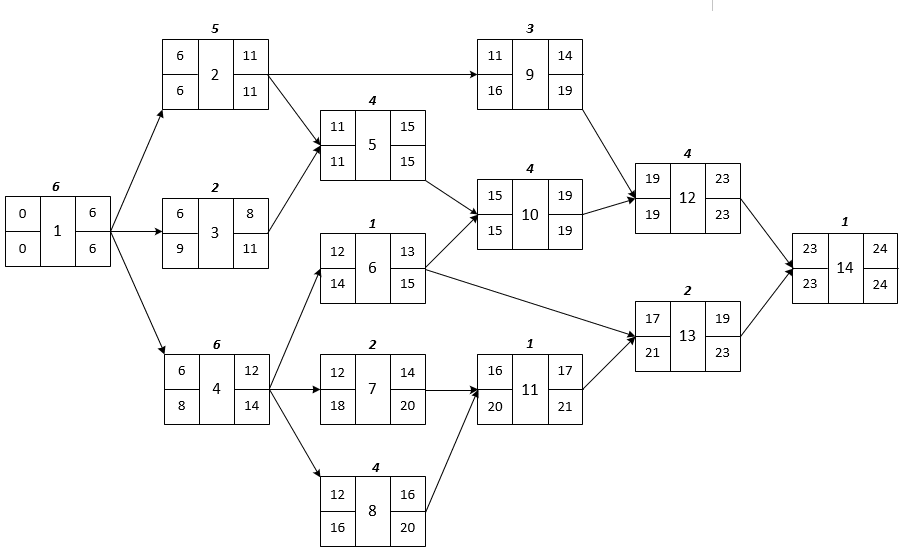
The Entire Process
The Complete Graph
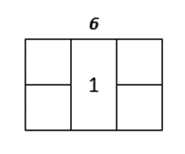
Visualization for Task 1
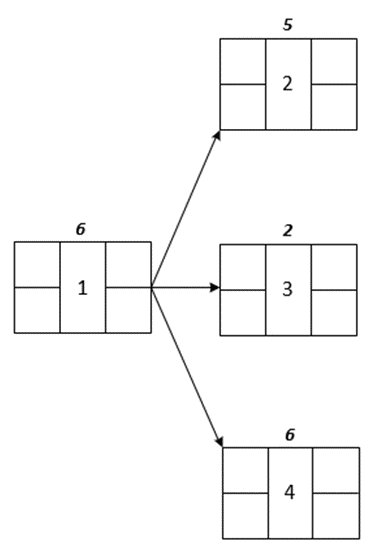
Visualization for Tasks 2, 3, and 4
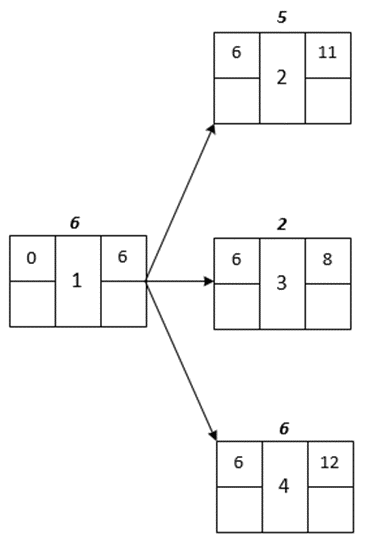
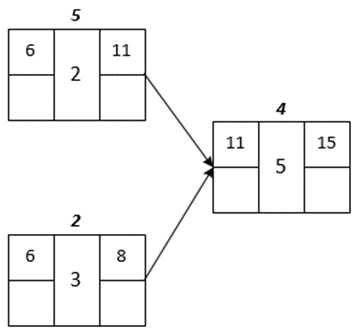
Visualization for Task 5
The Entire Process
The Entire Graph
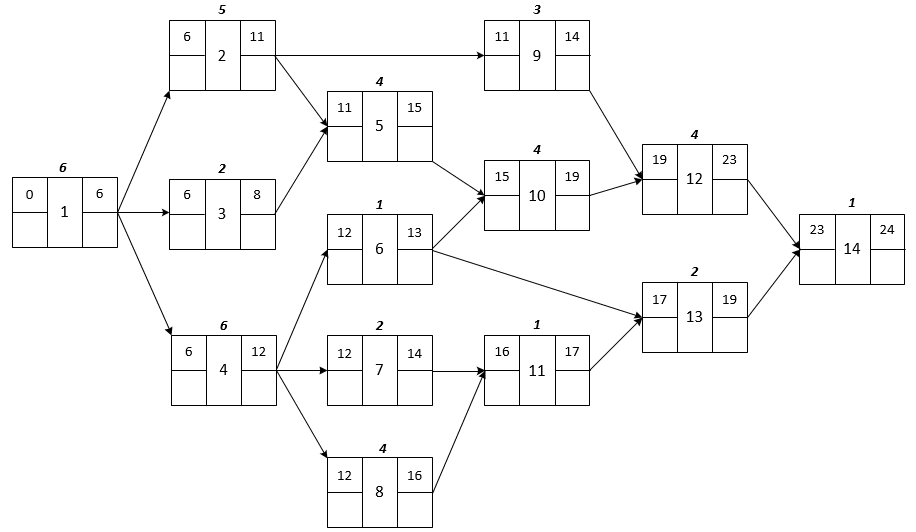
Visualization for Tasks 14
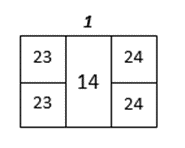
Visualization for Tasks 13
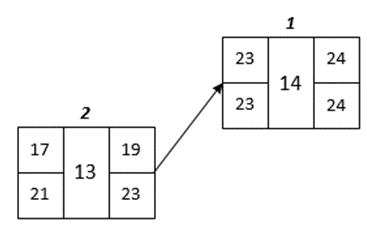
Visualization for Tasks 7 to 14
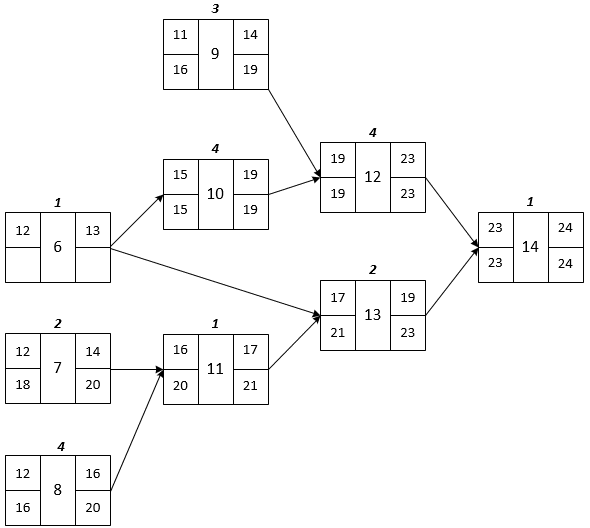
Task 6
\({\cal S}_6 = \{10, 13\}\)
\(C^"_6 = \min\{ I^"_{10}, I^"_{13} \} = \min\{15,21\} = 15\)
\(I^"_6 = C^"_6 - T_6 = 15 - 1 = 14\)
The Entire Process
The Entire Graph
The Entire Process
The Entire Graph
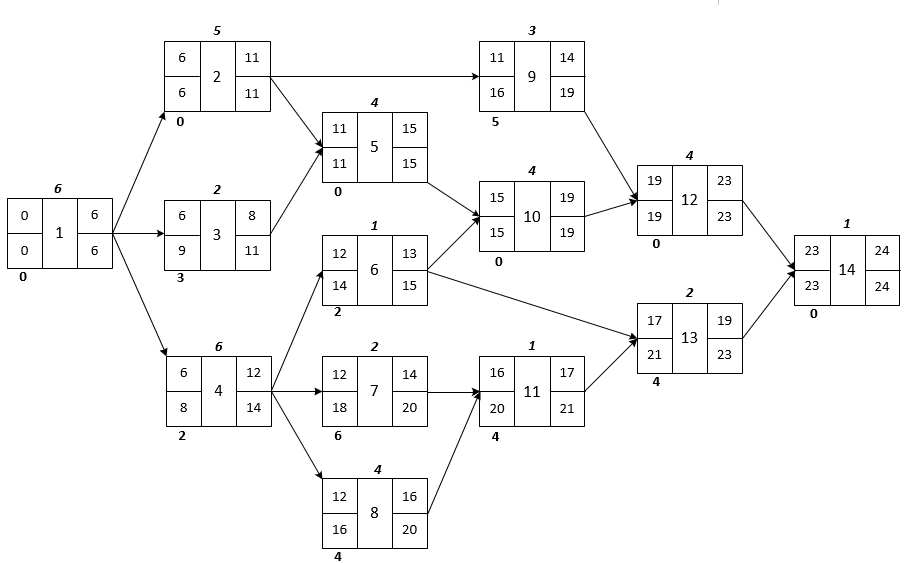
The Entire Process