Coordinate Systems for \(\mathbb{R}^{3}\)
An Introduction
|
|
Prof. David Bernstein
James Madison University
|
|
| Computer Science Department |
| bernstdh@jmu.edu |

|
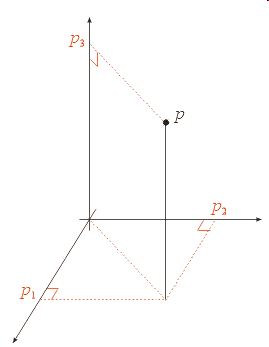
Rectangular/Cartesian Coordinates
- Reference Frames:
- An origin
- A basis (i.e., three linearly independent vectors)
- Directional conventions
- Quantities:
- Three linear (i.e., length) coordinates
- Visualization:
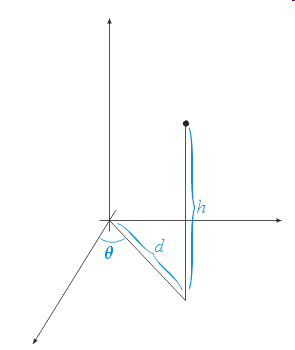
Cylindrical Coordinates
- Quantities:
- Polar coordinates in one plane (i.e., one angular and
one linear coordinate)
- Linear third coordinate
- Visualization:
Converting between Cylindrical and Cartesian
Notation
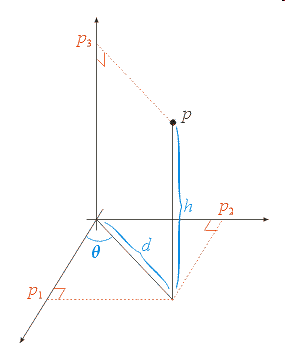
Converting from Cylindrical to Cartesian
- What We Know:
- \(\theta\), \(d\) and \(h\)
- Using the Right Triangle:
- \(\cos \theta = p_{1} / d\) so
\(p_{1} = d \cos \theta\)
- \(\sin \theta = p_{2} / d\) so
\(p_{2} = d \sin \theta\)
- \(p_{3} = h\)
Converting from Cartesian to Cylindrical
- What We Know:
- Using the Right Triangle:
- \(\tan \theta = p_{2} / p_{1}\) for \(p_{1} \gt 0\)
so \(\theta = \tan^{-1} p_{2} / p_{1}\)
- Using the Norm:
- \(d = \sqrt{p_{1}^{2} + p_{2}^{2}}\)
- By Definition:
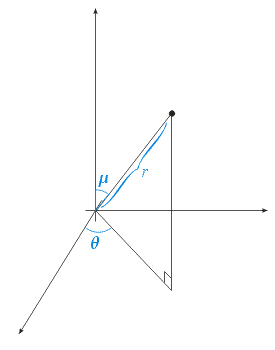
Spherical Coordinates
- Quantities:
- Two angular coordinates
- One linear coordinate
- Visualization:
Converting between Spherical and Cartesian Coordinates
Notation
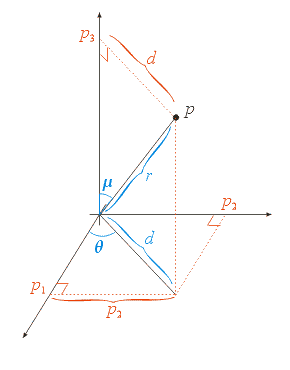
Converting from Spherical to Cartesian
- What We Know:
- \(\theta\), \(\mu\) and \(r\)
- Finding \(d\):
- \(\sin \mu = d / r\) so
\(d = r \sin \mu\)
- Finding \(p\):
- \(\cos \theta = p_{1} / d \) so
\(p_{1} = d \cos \theta = r \sin \mu \cos \theta\)
- \(\sin \theta = p_{2} / d \) so
\(p_{2} = d \sin \theta = r \sin \mu \sin \theta\)
- \(\cos \mu = p_{3} / r \) so
\(p_{3} = r \cos \mu\)
Converting from Cartesian to Spherical
- What We Know:
- Finding \(d\):
- \(d = \sqrt{p_{1}^{2} + p_{2}^{2}}\)
- Finding \(r\):
- \(r = ||\bs{p}|| = \sqrt{p_1^2 + p_2^2 + p_3^2}\)
- Using the Right Triangles:
- \(\tan \theta = p_{2} / p_{1}\)
so \(\theta = \tan^{-1} p_{2}/p_{1}\)
- \(\cos \mu = p_{3} / r\)
so \(\mu = \cos^{-1} \frac{p_{3}}{||\bs{p}||}\)