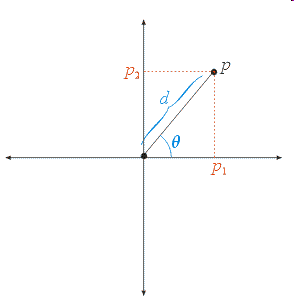Coordinate Systems for the Plane

Coordinate Systems for the Plane
An Introduction

Prof. David Bernstein
James Madison University

Computer Science Department

bernstdh@jmu.edu

Getting Started

Coordinates:
- Quantities that designate the position of a point in relation to a given reference frame.
The Quantities:
- Can be linear and/or angular

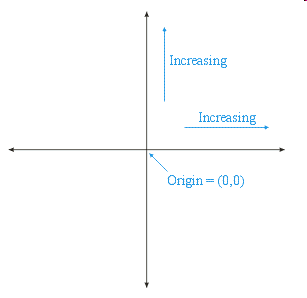
Rectangular/Cartesian Coordinates

Reference Frames:
- An origin
- A basis (i.e., an appropriate number of linearly independent vectors)
- Directional conventions
The Traditional Reference Frame for the Plane:
- The origin is at the center
- The basis consists of the horizontal and vertical axes
- Positive values in the "north east" quadrant

Visualizing Rectangular/Cartesian Coordinates

The Plane

Visualizing Rectangular/Cartesian Coordinates (cont.)

A Discretization

Visualizing Rectangular/Cartesian Coordinates (cont.)

Nerd Humor

(Courtesy of xkcd)

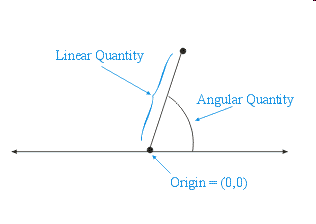
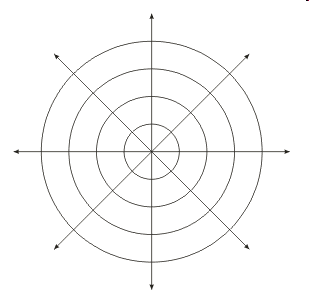
Polar Coordinates for the Plane

The Reference Frame:
- An origin at the center
- An angular rotation around the origin and a linear distance from the origin
- Counterclockwise is positive; North is positive
The Angular Quantity:
- Can be measured in degrees of radians

Visualizing Polar Coordinates

The Plane

Visualizing Polar Coordinates (cont.)

A Discretization

Converting between Polar and Cartesian Coordinates

Notation

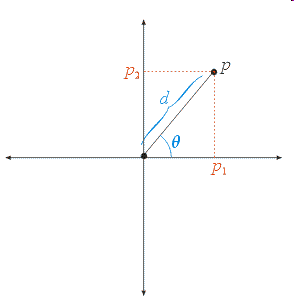
Converting from Polar to Cartesian

What We Know:
- \(\theta\) and \(d\)
Using the Right Triangle:
- \(\cos \theta = p_{1} / d\) so \(p_{1} = d \cos \theta\)
- \(\sin \theta = p_{2} / d\) so \(p_{2} = d \sin \theta\)

Converting from Cartesian to Polar

What We Know:
- \(\bs{p}\)
Using the Right Triangle:
- \(\tan \theta = p_{2} / p_{1}\) for \(p_{1} \gt 0\) so \(\theta = \tan^{-1} p_{2} / p_{1}\)
Using the Norm:
- \(d = ||\bs{p}||\)