|
Computational Geometry
An Introduction (in 2D) |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
|
Computational Geometry
An Introduction (in 2D) |
|
Prof. David Bernstein |
| Computer Science Department |
| bernstdh@jmu.edu |
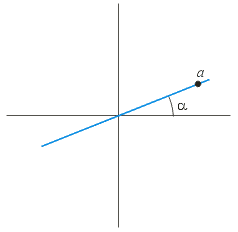
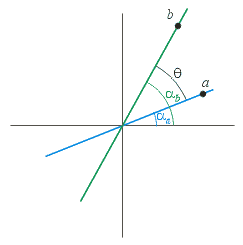
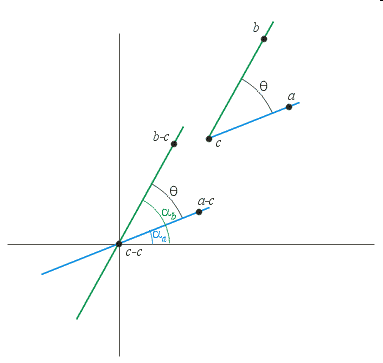
The Minimum Distance from a Point to a Ray
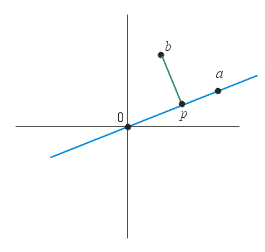
One Case
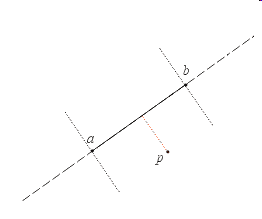
Another Case
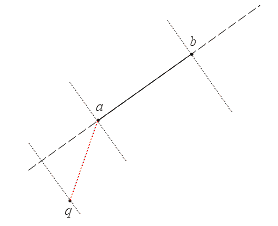
Distinguishing Between Cases - One Method
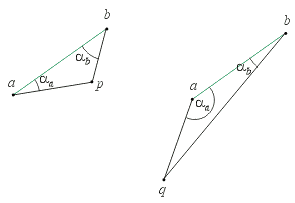
Distinguishing Between Cases - Another Method
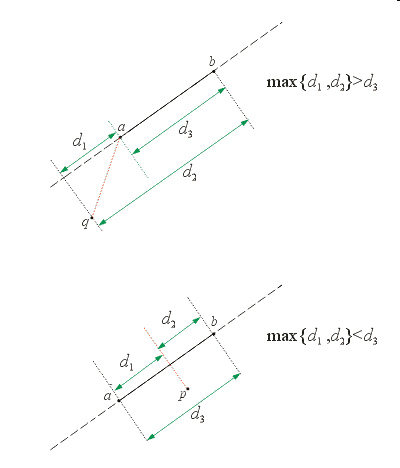
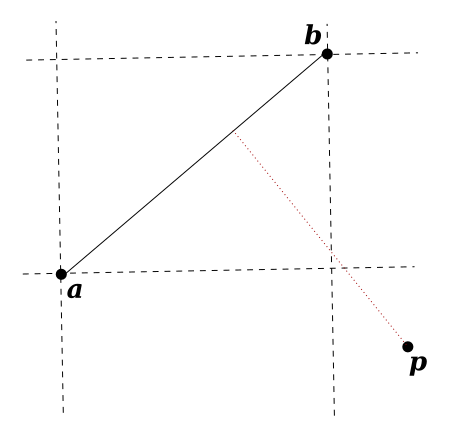
A Surprising Example - \(p\) Is Outside the Bounds of \(a\) and \(b\)