|
Lighting 3D Shapes
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
Lighting 3D Shapes
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |













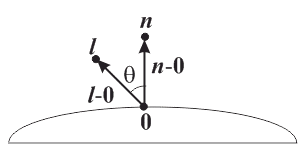






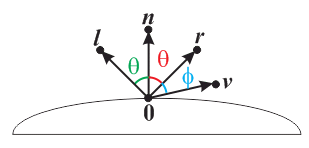






















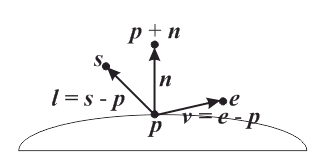








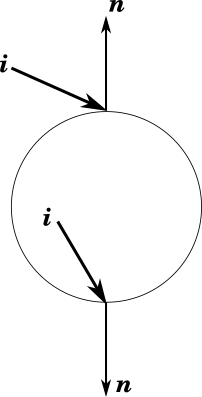
Understanding the Transmission/Refraction Angle
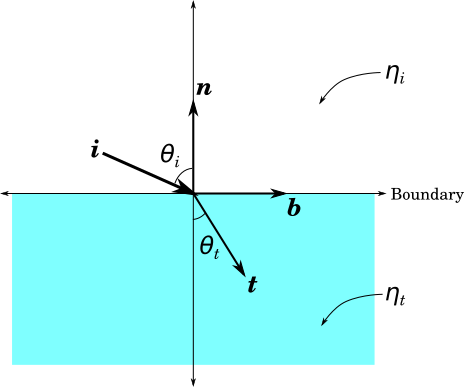
Where \(\eta_i\) and \(\eta_t\) denote the index of refraction of the initial medium and transmitting medium, respectively, \(\bs{n}\) denotes the normal vector, and \(\bs{b}\) is chosen so as to form a basis with \(\bs{n}\) (i.e., \( \bs{b} = \frac{\bs{i} + \cos(\theta_i)\bs{n}}{\sin(\theta_i)}\)).