

|
Hidden/Visible Objects in 3D
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |



|
Hidden/Visible Objects in 3D
An Introduction |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |







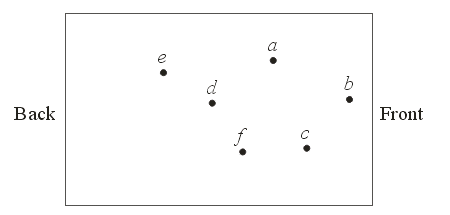











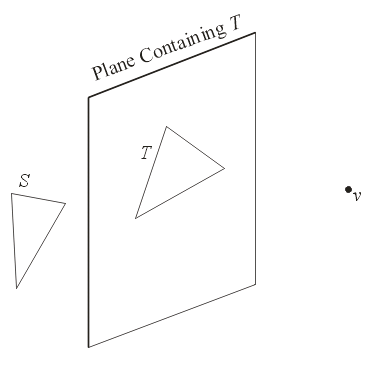




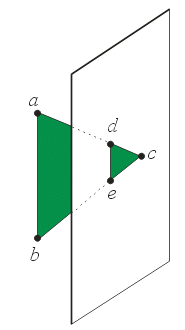


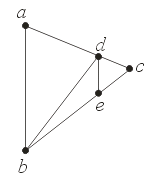




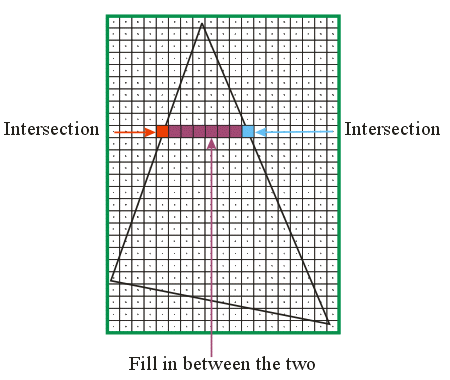






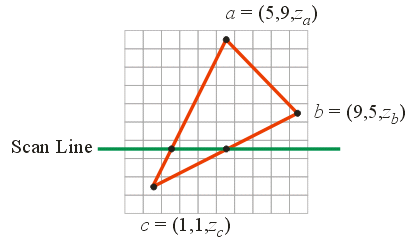


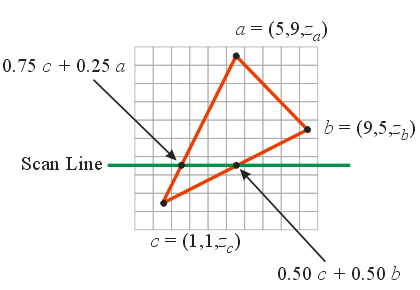


\(0.75 [1 \;\; 1 \;\; 10]^T + 0.25 [5 \;\; 9 \;\; 20]^T =\)
\([0.75 \;\; 0.75 \;\; 7.50]^T + [1.25 \;\; 2.25 \;\; 5.0]^T =\)
\([2.00 \;\; 3.00 \;\; 12.50]^T\)
\(0.50 [1 \;\; 1 \;\; 10]^T + 0.50 [9 \;\; 5 \;\; 20]^T =\)
\([0.50 \;\; 0.50 \;\; 5.00]^T + [4.50 \;\; 2.50 \;\; 10.0]^T =\)
\([5.00 \;\; 3.00 \;\; 15.00]^T\)









