|
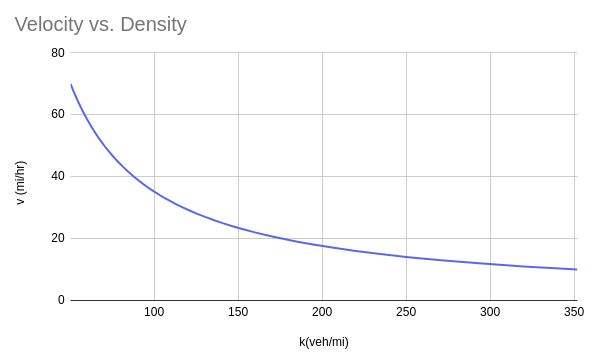
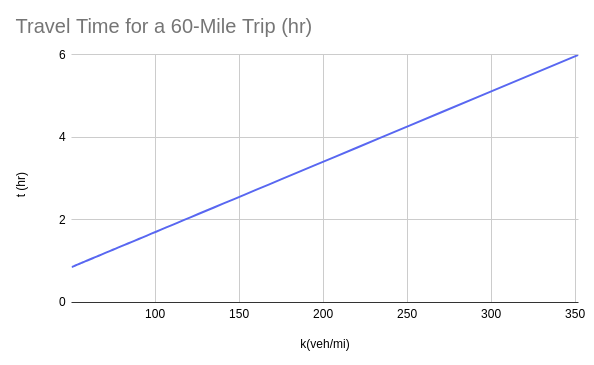
The Driver's "Rule of Thumb"
Understanding the Implications |
|
Prof. David Bernstein
|
| Computer Science Department |
| bernstdh@jmu.edu |