Analytic Geometry
An Introduction to Shapes in the Plane
|
|
Prof. David Bernstein
James Madison University
|
|
|
Computer Science Department
|
|
bernstdh@jmu.edu
|

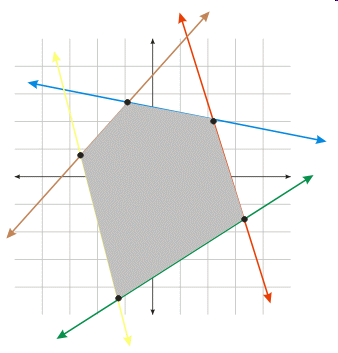
Intersection of Lines (cont.)



- A Common Special Case:
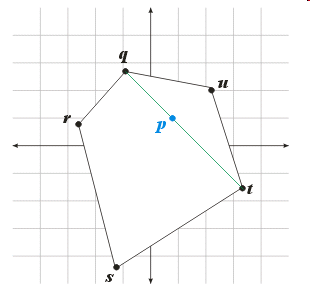
- \(\bs{v} = \bs{q} - \bs{p}\) (i.e., the line segment
with endpoints \(\bs{p}\) and \(\bs{q}\))
- \(\bs{w} = \bs{s} - \bs{r}\) (i.e., the line segment
with endpoints \(\bs{r}\) and \(\bs{s}\))
- Intepreting the Results:
- If \(\lambda \in [0,1]\) and \(\mu \in [0,1]\)
then the line segments defined by \(p,q\) and
\(r,s\) intersect.
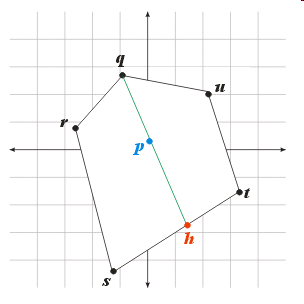
In this case, the two line segments intersect at the point
\((1-\lambda)\bs{p} + \lambda \bs{q}\) or, equivalently,
the point \((1-\mu)\bs{r} + \mu \bs{s}\)
- If \(\lambda \not\in [0,1]\) or \(\mu \not\in [0,1]\)
then the line segments defined by \(p,q\) and
\(r,s\) do not intersect but the line and line segment
(or vice versa) do intersect.
There's Always More to Learn