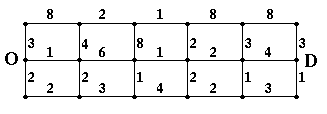
Figure 1. A simple network
Algorithms for finding the "best" route/path over a network have been around for many years. However, these algorithms are often not well-suited to providing route guidance because they are not very flexible. One issue that arises is that drivers frequently would like to be given several alternatives. It turns out that this is not as easy as it seems.
Consider the simple network shown in Figure 1 in which the numbers next to the links represent travel times (in minutes).

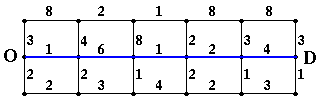
The fastest route from O (your origin) to D (your destination) is shown in blue in Figure 2. It has a total travel time of 14 minutes.
However, after you are given this route you decide that you would also like a good alternative. One natural approach is to calculate the second fastest route. This route is shown in red in Figure 3 and also has a travel time of 14 minutes.
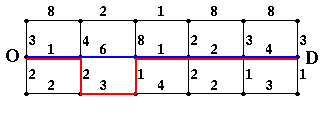
Unfortunately, many people are not really satisfied with this alterantive because it is so similar (i.e., has so many links in common) with the original route.
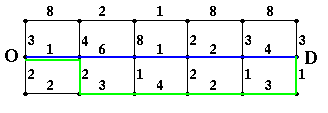
As a result, we have developed an algorithm for finding alternative routes that have "few" links in common with the fastest route. We call such routes similar. Returning to the above example, the fastest 1-similar route (i.e., the fastest route with at most one link in common with the original fastest route) is shown in Figure 4 in green.
A number of resources that consider this problem are currently available on this site, including:
For information about a this activity, feel free to contact the relevant faculty/students directly.