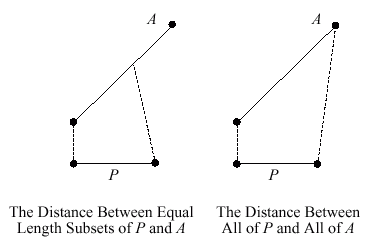
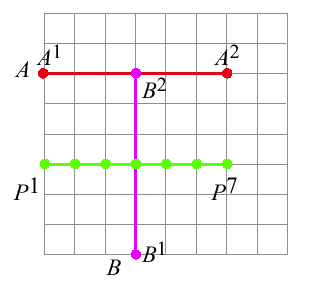
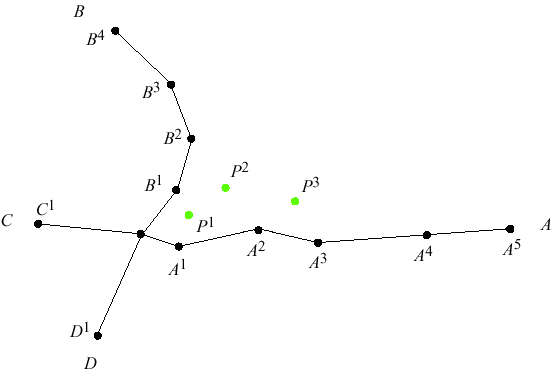
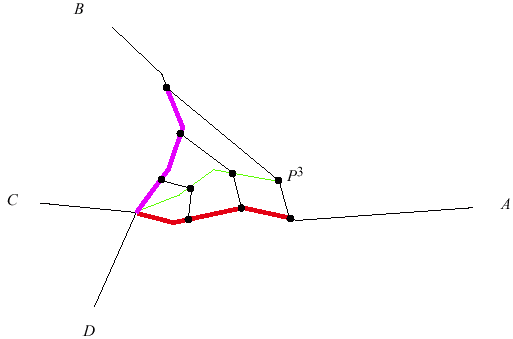
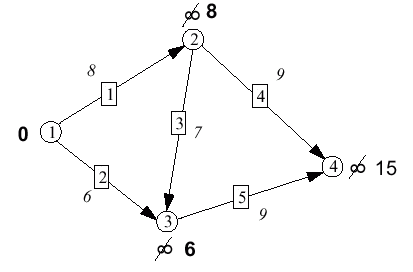
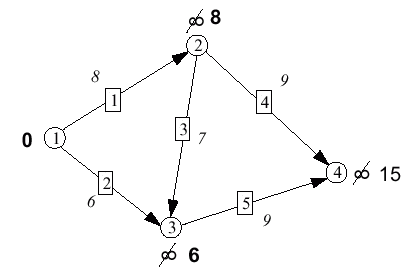
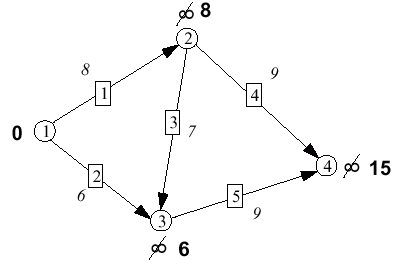
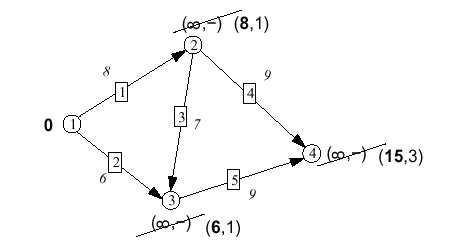
In-Vehicle Navigation Systems

In-Vehicle Navigation Systems
An Introduction

Prof. David Bernstein
James Madison University

JMU Chapter of the ACM

Fall 2001

Overview

In-Vehicle Navigation Systems
Vehicle Location Algorithms
Map-Matching Algorithms
Route Finding Algorithms

In-Vehicle Navigation Systems

First Generation:
- Provide the user with a map and the ability to search
Second Generation:
- Provide both a map and the user's current location/position
Third Generation:
- Provide a map, the user's location, and directions of some kind

Required Technologies

First Generation:
- Microprocessor
- Mass storage device
- Graphical display device (probably color)
- Input devices (e.g., keyboard, pointing device)
- Algorithms for manipulating raster/vector data
Second Generation:
- Positioning hardware (e.g., GPS, dead-reckoning)
- Positioning algorithm
Third Generation:
- Map-matching algorithm
- Route-finding algorithm

GPS: Satellites

24 satellites in 6 evenly-spaced orbits
Each satellite circles the Earth every 11 hours 58 minutes
The orbital radius of these satellites is 26,560km

GPS: Coordinate Systems

Geocentric (i.e., origin at the center of the Earth)
Earth-Centered-Earth-Fixed (Cartesian)

Triangulation Algorithms

Notation:
- T^j is the "actual" time satellite j transmits
- T is the "actual" time that the signal is received
Some Fundamentals:
- Distance: c ^. ^Delta; T^j (where c is the speed of light)

Triangulation Algorithms (cont.)

The System to Solve:

Triangulation Algorithms (cont.)

An Observation:
- The clock on the GPS receiver differs from the correct time by ^delta;
The New System to Solve:

Triangulation Algorithms (cont.)

A Linearization:
- Recall that the first-order Taylor series expansion of a function f (around the point a) is given by:
- f(a) + f'(a)(x - a)
- For the system of three variables:
Elements of the Linearized System:

Longitude, Latitude and Altitude

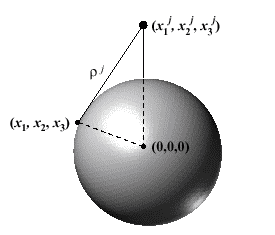
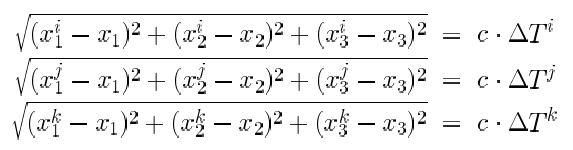
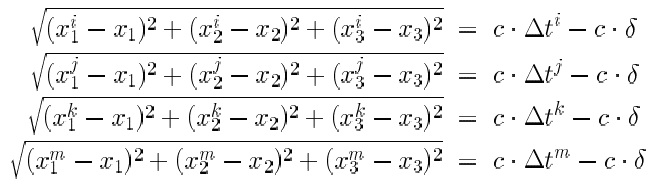
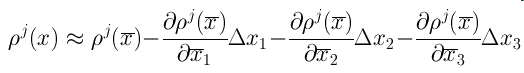
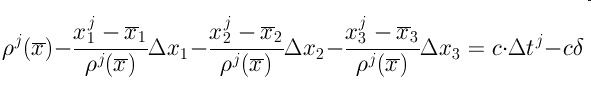
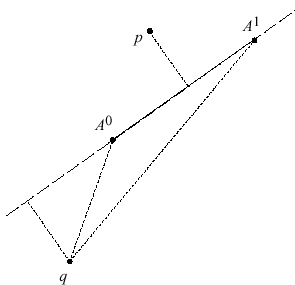
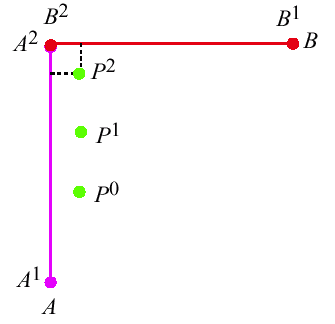
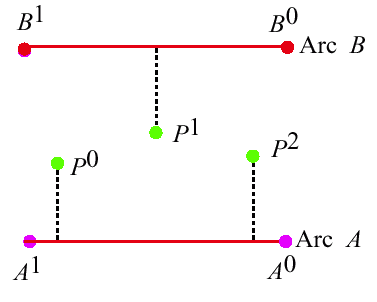
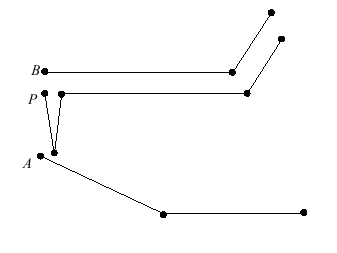
Ellipsoidal and Cartesian Coordinates

Long., Lat. and Alt. (cont.)

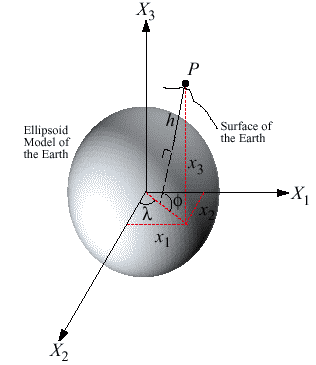
Changing Coordinate Systems

Long., Lat. and Alt. (cont.)

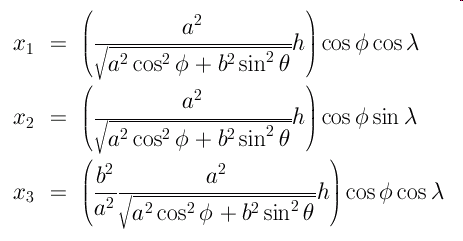
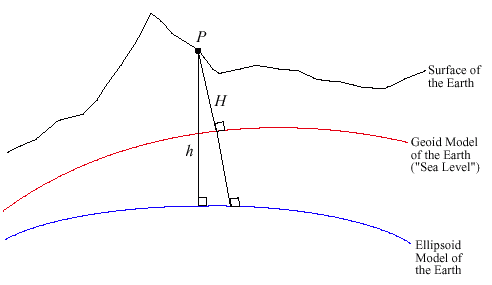
A Closer Look at Altitude

The Map-Matching Problem

Point-to-Point Matching

The Idea:
- Match P^t to the "closest" node or shape point
A Difficulty:

Point-to-Curve Matching

The Idea:
- Identify the arc that is closest to P^t
One Approach:

Point-to-Curve Matching (cont.)

One Difficulty:

Point-to-Curve Matching (cont.)

Another Difficulty:

Curve-to-Curve Matching

The Idea:
- Find the arc that is closest to the piecewise linear curve, P defined by the points P⁰, P¹, ^cdots;, P^m
A Difficulty:

Curve-to-Curve Matching (cont.)

Another Approach:
- Use the "total" distance
A Difficulty:

Curve-to-Curve Matching (cont.)

Another Approach:
- "Correct" for differences in length
A Difficulty:

Using Topological Information

Using Topology (cont.)

Route Finding

What We Now Know:
- Where we are
What We Need:
- How to get to our destination

A Route Finding Algorithm

A Route Finding Algorithm (cont.)

Make the origin the working node
While the working node is not the destination do the following:
- Update the temporary labels.
- Find which node should be permanent and make it the new working node.

Updating Temporary Labels

For all nodes that are reachable from the working node:
- Calculate the distance to this node through the working node.
- If This distance is less than the nodes current label:
  - Set the nodes label equal to this distance.
  - Set the nodes predecessor equal to the working node.

Making a Label Permanent

For all nodes with temporary labels:
- Find the node with smallest temporary label.
Make the status of this node permanent.
Set the working node equal to this node.

Research on Algorithms

Alternatives to the Best Path
Routing via Intermediate "Points"
Incorporating "Time" and "Tolls"
Algorithms for "Very Small" Devices
Routing for En Route Commerce

Research on Algorithms (cont.)

Incorporating Real-Time Traffic Information
Forecasting Traffic Conditions
Using Vehicles as Probes

Research on Architectures

Parking Information and Reservations
Transit Information Provided On Vehicles
Transit Information Provided at Stops

There's Always More to Learn