
| (1) | _____ |
A /27 CIDR network contains at most: |
|
||
| (2) | _____ |
The mask 11111111.11111111.11111000.00000000
corresponds to a: |
|
| Persistence (in the sense of HTTP) |
| Graph |

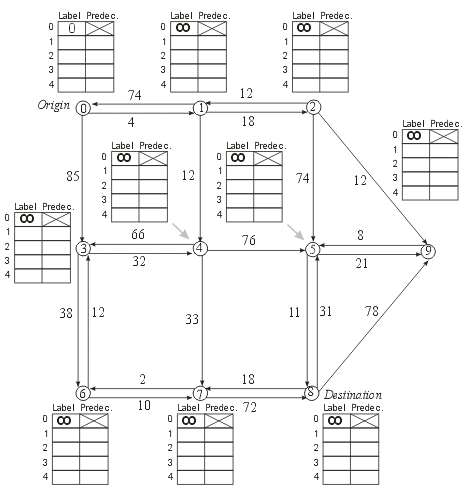
calculate the "shortest" path from vertex/node 0 to vertex/node 8 using the Dijkstra's label setting algorithm (as discussed in lecture). Show your work in the tables next to each vertex/node (i.e., each time you change the label associated with a vertex/node you must add a row to the associated table that contains the new label and the new predecessor).
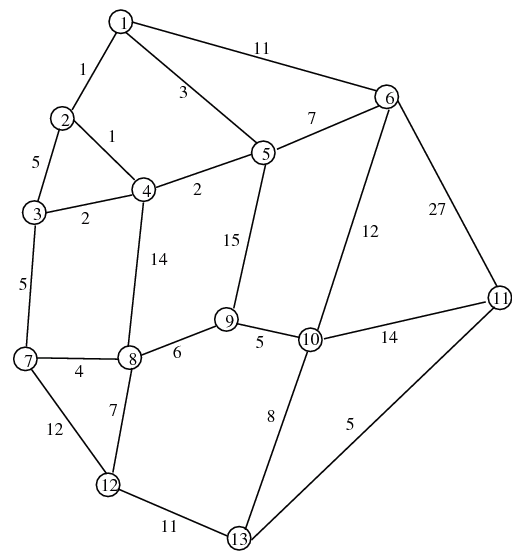
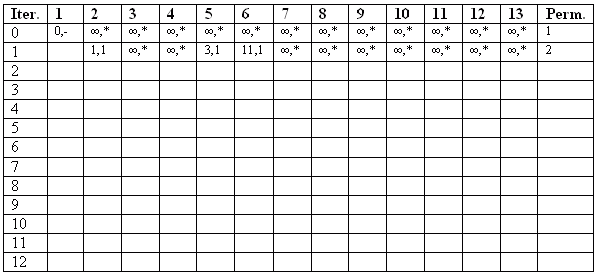
Show that the "shortest" path from vertex/node 1 to vertex/node 11 is 1-5-6-10-13-11 which has a "length" of 35. You must use Dijkstra's label setting algorithm (as discussed in lecture). Show all of your work in the table below (where iterations 0 and 1 have already been completed).
Now, suppose that a message of 00 is transmitted with a
(correct) parity bit of 0.
What is the probability that the message is
corrupted and that the error is not detected? (Hint: Carefully
list all of the outcomes/events and assign probabilities to them.)
Copyright 2013