Lecture 23 - November 13, 2007

First we reviewed the desired answer for writing a Snobol assignment statement for the binary tree below using the previously defined Data statement: DATA('BNODE(VALUE,LSON,RSON)')

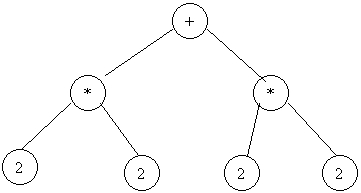
Bnode('+', Bnode('*', Bnode(2, null, null), Bnode(2,null,null)), Bnode('*', Bnode(3, null, null), Bnode(3,null,null)))

Then we looked at a program containing a function to traverse a binary tree in PREORDER and the output of that program.

DEFINE('LLIST(N)') :(LLIST_END)

LLIST OUTPUT = DIFFER(N) VALUE(N) :F(RETURN)

LLIST(LSON(N))

LLIST(RSON(N)) :(RETURN)

LLIST_END

DATA('BNODE(VALUE,LSON,RSON)')

N = BNODE('+',BNODE('X'), BNODE('Y'))

P = BNODE('+', BNODE('*',BNODE(5), BNODE(7)),BNODE('-',BNODE(16),BNODE(7)))

LLIST(N)

OUTPUT = ' '

LLIST(P)

OUTPUT = ' '

Q = Bnode('+', Bnode('*', Bnode(2, null, null), Bnode(2,null,null)),

+ Bnode('*', Bnode(3, null, null), Bnode(3,null,null)))

LLIST(Q)

END

Then we went back to talking about LISP

Remember:

The cdr of a list is ALWAYS a list

Everything in Lisp is a list or an atom

Here are some built-in functions we talked about and tested. KNOW THEM!

Note that some of them behave differently with different parameters and/or different parameter types.

> (+ 2 3)

> (- 3 7)

> (* 9 8)

> (/ 6 3)

> (/ 5 3)

> (a b c)

> '(a b c)

> (quote (a b c))

> (setq a (+ 3 7))

> a

> (car '(a b c))

> (car '( (a) b c))

> (cdr '(a b c))

> (cdr '( (a) b c))

> (car (cdr '(a b c)))

> (cadr '(a b c))

> (cadr (cdr '(a b c)))

> (list '(1 2 3))

> (type-of 7)

> (type-of 1.2)

> (type-of '(1 2 3))

> (type-of 7/2)

> (abs 3.6)

> (abs -3.6)

> (round 3.6)

> (round 3.2)

> (expt 3 4)

> (exp 3)

> (atom '(1 2 3))

> (atom 1)

> (numberp a)

> (numberp b)

> (listp '(1 2 3))

> (listp b)

> (numberp 'a)

> (floatp 4.5)

> (characterp #\a)

> (listp 'c)

> (listp 3)

> (setq b '(1 2 3)

> b

> (type-of 6)

> (type-of '(a b c))

> (type-of 7.2)

> (type-of 7/2)

; relational operators

> (> 7 8)

> (> 6 2.5)

> (< 2 3)

> (<= 7 9)

> (>= 7 9)

> (/= 7 9)

; three prints - the first two print ;the output twice

> (print '(a b c))

> (princ '(a b c))

> (pprint '(a b c))

> (cls)

; extracting parts of lists

> (setq mylist '(1 2 3 a b n c 4 I u j)

> (car mylist)

> (cdr mylist)

> (car (cdr mylist))

> (cdr (cdr mylist))

> (cdr '( ))

> (caar mylist)

> (cadr mylist)

> (cddr mylist)

> (cdddr mylist)

> (caddr mylist)

> (cadddr mylist)

; here's a way to see what your user defined functions are doing

>(trace functionName)

> (trace +)

> (untrace functionName)

> (untrace)

; here are some predicates that ; combine lists

> (list 'a 'b)

> (cons 'c '(1 2 3))

> (append '(1 2 3) '(4 5 6)

; three different equality tests

; behave differently with different

; types of arguments

> (eq 6 6)

> ( equal 6 6)

> ( = 6 6)

> (defun fName (parameterList)

( )

)

; load works if file in same directory

> (load "fib3.lsp")

; loading "fib3.lsp"

T

Here's the cube function we defined in class

(defun cube (p)

(* p p p)

)

; Here's a recursive function using the "cond" I promised

(defun fib (x)

(cond

( (= x 1) 1)

( (= x 2) 1)

(t (+ (fib (- x 1)) (fib (- x 2) ) ) )

)

)

Here's how the "cond" behaves

It's a little like a Pascal case statement in that it has a series of conditions which are evaluated and an action which is performed if the condition evaluates to true. The last condition ALWAYS evaluates to true because we simply place a T as the test.