Lecture 21 – November 9^th

A heap represents a binary tree stored in an array.

Note that a heap does NOT represent a binary search tree.

There are two types of heaps, a min-heap and a max-heap.

In both types of heaps, the children of a node n are stored in positions 2n and 2n+1.

In a min-heap, the value stored in node n is less than the value stored in either of n’s children.

In a max-heap, the value stored in node n is greater than the value stored in either of n’s children.

In the example we did in class, we had already stored the values we wanted to put into the min-heap in an array. This is not necessary. The heap can be built by inserting each value in its proper place

In the example that follows you will see the array filled and the corresponding tree shown as the values are entered one at a time.

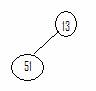
Here are the 8 values to be entered: 13, 51, 9, 7, 21, 10, 4, 8

1	2	3	4	5	6	7	8
13

1	2	3	4	5	6	7	8
13	51

1	2	3	4	5	6	7	8
13	51	9
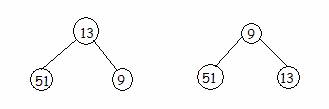
9	51	13

1	2	3	4	5	6	7	8
9	51	13	7
9	7	13	51
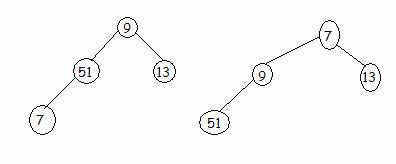
7	9	13	51

Two swaps necessary:

first node in position 4 (2*2)and node in position 2

second node in position 2 and 1

1	2	3	4	5	6	7	8
7	9	13	51	21

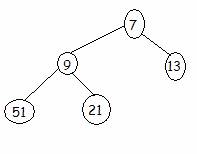
No swaps necessary node in position 5 (2*2+1) is bigger than its arent

1	2	3	4	5	6	7	8
7	9	13	51	21	10
		10			13

One swap necessary, the item in position 6 (2*3) is swapped with item in position 3

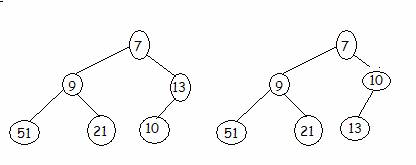
1	2	3	4	5	6	7	8
7	9	10	51	21	13	4
		4				10
4		7

Two swaps necessary

position 7 (2*3+1) and position 3

position 3 (2*1+1) and position 1

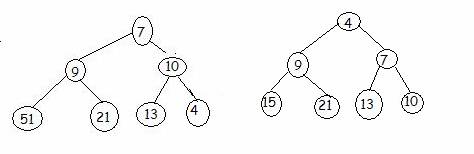
1	2	3	4	5	6	7	8
4	9	7	15	21	13	10	8
4			8				15
	8		9

Two swaps are necessary

position 8 (2*4) with position 4

position 4(2*2) with position 2

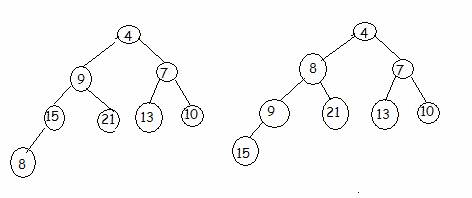
The min-heap has now been built

The children of each node n are in positions 2n and 2n1

Now we are ready to sort the heap