October 19 Homework
Name ________________________
1. Draw the circuit (logic network) for the Boolean expression
(x1x2+ x3)' + x3
2. Find the canonical sum-of-products form for the truth function in the table below. ( Do not simplify it).
x1x2x3’ + x1x2’x3’
|
x1 |
x2 |
x3 |
f(x1 ,x2 ,x3 ) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
3 Write the minimal sum-of-products form for the Karnaugh map of the figure below
|
|
x1 x2 |
x1x2' |
x1'x2' |
x1'x2 |
|
x3x4 |
|
1 |
|
|
|
x3x4' |
|
1 |
1 |
1 |
|
x3'x4' |
1 |
1 |
1 |
|
|
x3'x4 |
|
1 |
|
|
x1x3’x4’ + x1’x3x4’+x2’x4’ +x1x2’
4. Write the following base 10 numbers as unsigned numbers in base 16
|
base 10 |
base 2 |
base 8 |
base 16 |
|
2472 |
100110101000 |
4650 |
9A8 |
|
24.72 |
011000.10111000 |
30.56 |
18.B8 |
|
2.472 |
10.011110 |
2.36 |
2.78 |
|
.2472 |
0.001111 |
0.17 |
0.3C |
5. Write the following base 10 numbers in ones complement, twos complement and sign magnitude notation using 7 bits.
|
base 10 |
sign magnitude |
ones complement |
twos complement |
|
+27 |
0011011 |
0011011 |
0011011 |
|
-28 |
1011100 |
1100011 |
1100100 |
|
+17 |
0010001 |
0010001 |
0010001 |
|
-34 |
0100010 |
1011101 |
1011110 |
6. Using prepositional logic (use the tables in your book), prove that each of the following arguments is valid
A' ^ (B -> A) -> B'
1. A’ hyp
2.
B -> A hyp
3. B’ 1,2
modus tollens
(A'-> B') ^ (A -> C) -> (B -> C)
1. A’ -> B hyp
2.
A -> C hyp
3.
B hyp
4.
B -> A 1,
contrapositive
5.
C 2.4 hypothetical syllogism
7.Using propositional logic, prove that each argument is value. Use the statement letters shown.
If Jane is more popular, then she will be elected. If Jane is more popular, then Craig will
resign. Therefore, if Jane is more
popular, she will be elected and Craig will resign. J,
E, C
[ (J
-> E) ^ (J-> C)]
-> (J -> (E ^ C))
1. J -> E hyp
2. J-> C hyp
3. J hyp
4.
E 1,3, modus ponens
5.
C 2,3, modus ponens
6. E^C 4,5 con
8. Using predicate logic, prove that the following argument is value. Use the predicate symbols shown.
Some plants are flowers. All flowers smell sweet. Therefore, some plants smell sweet. P(x), F(x), S(x)
($x)[P(x) Ù F(x)] Ù ("y)[(F(y) → S(y)] → ($x)[P(x) ÙS(x)]
1.
($x)[P(x) Ù F(x)] hypothesis
2.
("y)[(F(y) → S(y)] hypothesis
3.
P(a) Ù F(a ) 1,
e.i. (existential instantiation)
4.
(F(a) → S(a) 2. u.i. (universal
instantiation)
5.
F(a) 3. simplification
6.
S(a) 5,4 mp
(modus ponens)
7.
P(a) 3. simplification
8.
P(a) Ù S(a) 6,7 conjunction
9.
($x)[P(x) ÙS(x)] 8 e.g.
(existential generalization)
9. Prove that the product of two even integers is even.
x = 2m
y = 2n
xy = (2m)(2n) = 4mn = 2(2mn)
so xy has the form 2k where k is an integer and therefor xy is even
10. Using mathematical induction, prove that the following statement is true for every positive integer n.
2 + 6 + 10 + … + (4n-2) = 2n2
P(1): 4*1 – 2 = 2(1)2 or 2
P(k): 2 + 6 + 10 + ... +
(4k – 2) = 2k2
Show P(k+1)
: 2 + 6 + 10 + ... + (4k -2 ) + [4(k+1)
-2)] = 2(k+1)2
Starting with the left side
2 + 6 + 10 + ... + (4k -2 ) + [4(k+1) -2)] =
2k2 + [4(k+1) -2)] =
2k2 + 4k + 4 – 2 =
2k2 + 4k + 2 =
2(k2
+ 2k + 1) =
2(k +1)2
Ending with the desired right side
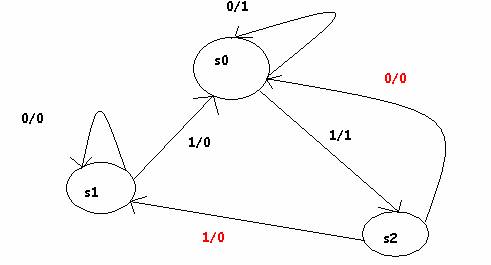
11. Given the state table below for a given machine, draw the state diagram and compute the ouput sequence for the following input sequence 10001
|
Present state |
input |
next state |
output |
|
s0 |
0 |
s0 |
1 |
|
s0 |
1 |
s2 |
1 |
|
s1 |
0 |
s1 |
0 |
|
s1 |
1 |
s0 |
0 |
|
s2 |
0 |
s0 |
0 |
|
s2 |
1 |
s1 |
0 |
start at s0
output is 10111
state diagram below
12. For the following grammar G, generate enough valid sentences in the language so that you can tell in English what the language consists of. (show the sentences you generate)
G = (V, VT, S, P) where V = {0,1,A,B,S} , VT = {0,1}, and P consists of
S -> 0
S -> 0A
A -> 1B
B -> 0A
B -> 0
S S S
\
/ \ / \
0 0 A
0 A
/ \ / \
1 B 1 B
| / \
0
0 A
/ \
1 B
\
0
The language consists of a 0
followed by as
many 1 0 pairs as desired.