Homework #18

=Homework #18

Turn this in at or before the exam. If you come by my office with it done, you can check your answers.

Study for test on Monday, November 21^st.

Chapter 7 – Relations

Chapter 8 – Graphs

Sequential circuits & flip-flops

Glance at Logic proofs

Study Algorithm 1 and Example 25 on page 526, and Figures 9 and 11 on page 527. The use the methods to perform a topological sort on the diagram in problem 27 on page 534.

One solution:

Find recipe - Buy seafood – buy groceries – steam rice – wash vegetables – cut ginger and garlic – wash shellfish – clean fish – make garnishes – chop water chestnuts – cut fish –cook in wok – arrange in platters – serve

Problem 4 on page 528 - tell why it is or is not a partial order.

being a partial order requires: reflexive, antisymmetric and transitive. This is not a partial order because it is not transitive. c is related to d and d is related to be but c is not related to b.

Problem 16b on page 532.

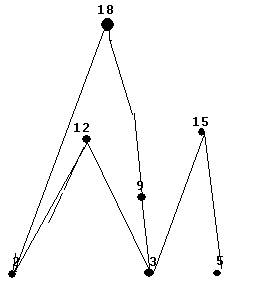
Problem 20 on page 529.

{ (a,a), (a,b), (a,c), (a,d), (a,e), (b,b), (b,d), (b,e), (c,c), (c,d), (d,d), (e,e)}

Problem 4 on page 544.

multigraph

Problem 14 on page 544.

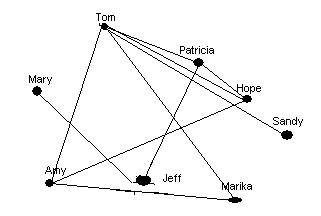
Problem 8 on page 554.

vertices 4

edges 8

indegree: a-2, b-3, c-2, d-1

outdegree: a-2, b-4, c-1, d-1

Problem 26 on page 555

it has 7 edges (by the handshaking theorem the sum of the degrees of the vertices is 2 times the number of edges in an undirected graph even if multiple edges and loops are present).

It also asked you to draw the graph…

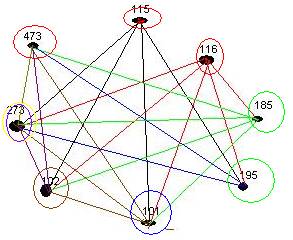
Problem 17 on page 620

This problem tells you which classes do NOT conflict. In order to determine the chromatic number you need to know which conflict.

	115	116	185	195	101	102	273	473
115	0	0	0					0
116	0	0						0
185	0		0	0
195			0	0	0	0
101				0	0
102				0		0
273							0
473	0	0						0

A solution: (red circles) 115, 473, 116

(green circles) 185, 195

(blue circle) 101

(brown circle) 102

(lavender circle) 273

5 different time slots are needed !!!

Problem 2 on page 563.

Vertex	Adjacent vertices
a	b,d
b	a,d,e
c	d,e
d	a,b,c
e	b,c

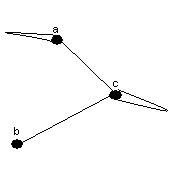
Problem 22 on page 564.

Look at figures 1 and 2 on page 578. They show the Konigsberg Bridge problem

	115	116	185	195	101	102	273	473
115	0	0	0					0
116	0	0						0
185	0		0	0
195			0	0	0	0
101				0	0
102				0		0
273							0
473	0	0						0

	115	116	185	195	101	102	273	473
115	0	0	0					0
116	0	0						0
185	0		0	0
195			0	0	0	0
101				0	0
102				0		0
273							0
473	0	0						0

	115	116	185	195	101	102	273	473
115	0	0	0					0
116	0	0						0
185	0		0	0
195			0	0	0	0
101				0	0
102				0		0
273							0
473	0	0						0