Homework # 17

due November 17^th

Name ___________________________

Section 7.3 – Representing Relations

Pages 494 to 496

1a 1 1 1

0 0 0

0 0 0

1b 0 1 0

1 1 0

0 0 1

2a 0 1 1 1

0 0 1 1

0 0 0 1

0 0 0 0

2b 1 0 0 1

0 1 0 0

0 0 1 0

1 0 0 0

4a { (1,1), (1,2), (1,4), (2,1), (2,3), (3,2), (3,3), (3,4), (4,1), (4,3), (4,4)}

4b {(1,1), (1,2), (1,3), (2,2), (3,3), (3,4), (4,1), (4,4)}

8 not reflexive, not irreflexive, synnetric, not antisymmetric, not transitive

10a matrix has 1000*1000 entries ; there are 1000 elements along the main diagonal which meet the desired criteria

Subtracting thos 1,000 elements leaves 1,000,000-1,000 or 999,000 elements

Half of those 999,000 or 499,500 also meet the criteria so the answer is 499,500 + 1,000 or 500,500

20.

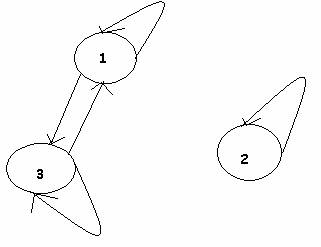
24 { (a,a), (b,a), (b,b), (c,c), (a,c), (b,c)}