CS 228 Exam 2 – November 21, 2005
Name
______________________
- 1. List the ordered pairs in the
relation R from A = {1, 3, 5, 7} to B = {2,4,6} where (a,b) Î R if and only if a > b. (5 points)
R =
{ (3,2), (5,2), (5,4), (7,2) ,
(7,4), (7,6)}
- Given the following relations on the
set { 1,2,3,4}, fill in the table below placing a check in the appropriate
column if the relation has that property.
(6 points)
|
Relations |
reflexive |
symmetric |
transitive |
irreflexive |
anti-symmetric |
|
{(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)} |
xx |
xxx |
xx |
|
|
|
{(2,4), (4,2)} |
|
xxx |
|
xxx |
|
|
{(1,3), (1,4), (2,3), (2,4), (3,1), (3,4)} |
|
|
|
xxx |
|
- Given the following sets and
relations (8 points)
A
= {2,4,5}
B
= {2,4,5,8}
R1
= { (2,2), (4,4), (5,5)}
R2
= {(2,2), (2,4), (2,5), (2,8)}
Complete the table
below
|
R1
∩ R2 |
{(2.2)} |
|
R1
Ụ R2 |
{(2,2), (2,4),(2,5), (2,8), (5,5), (4,4)} |
|
R1
–
R2 |
{ (4,4), (5,5)} |
|
R2
–
R1 |
{ (2.4), (2,5), (2,8)} |
- The 5-tuples in a 5-ary relation
represent these attributes of all people in the United States: name, Social Security number, street
address, city, state. Why is Social Security number the only reasonable
primary key? (5 points)
because it is the only attribute that is guaranteed to be unique. People can have the same name, the same street address, live in the same city and the same state.
- What do you obtain when you apply the
selection operator SC, where C is the condition (Project = 2) Ù (Quantity >= 12) to the database
below. (5 points)
|
Part-Number |
Project |
Quantity |
Color-Code |
|
1001 |
1 |
14 |
8 |
|
1092 |
1 |
2 |
2 |
|
1101 |
3 |
1 |
1 |
|
3477 |
2 |
25 |
2 |
|
4975 |
3 |
6 |
2 |
|
6984 |
4 |
10 |
1 |
|
9048 |
4 |
12 |
2 |
|
9191 |
2 |
80 |
4 |
|
|
|
|
|
|
|
|
|
|
|
3477 |
2 |
25 |
2 |
|
9191 |
2 |
80 |
4 |
- Under what conditions is a relation on
a set A called an equivalence relation?
(6
points)
A
relation on a set A is called an equivalence relation if it is reflexive,
symmetric and transitive
- Given the relation below on the set
{1,2,3,4}
{(1,2),
(1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)}
- draw the directed graph that
represents it (5 points)
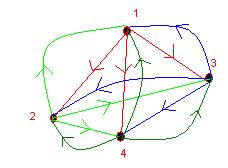
- represent it with a zero-one matrix.
(5 points)
|
|
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
1 |
1 |
|
2 |
1 |
0 |
1 |
1 |
|
3 |
1 |
1 |
0 |
1 |
|
4 |
1 |
1 |
1 |
0 |
- Draw the Hasse diagram for the "greater
than or equal to" relation on the set { 2, 4, 6, 8, 10} (5
points)
2
|
4
|
6
|
8
|
10
-
Given the Hasse diagram below representing a partial ordering
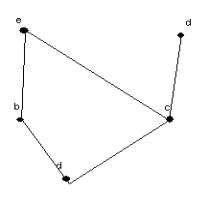
- list all the ordered pairs in the
partial ordering with the accompanying Hasse diagram (5 points)
{ (a,a), (b,b), (c,c), (d,d), (e,e), (a,b),
(a,c), (a,e), (a,d), (b,e), (c,d), (c,e)}
- provide a topologial sort. (5 points)
any of the following: a b c d e a c d b e a c b e d a b c e d
- Suppose that you are responsible for
scheduling the final exams for seven finals. The courses are numbered 1 through 7. Suppose that the following pairs of
courses have common students: 1
and 2, 1 and 3, 1 and 4, 1 and 7, 2 and 3, 2
and 4, 2 and 5, 2 and 7, 3 and 4, 3 and 6, 3 and 7, 4
and 5, 4 and 6, 5 and 6, 5 and 7, and 6 and 7.
- draw
the graph model (5 points)
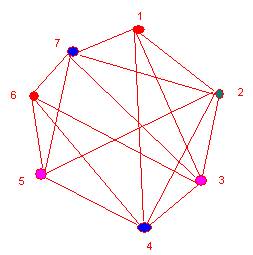
- determine
the number of time periods needed to avoid scheduling conflicts. (5 points)
4 time periods
are needed. A possible schedule would
pair: 1 and 5, 2 and 6,
4 and 7, and have 3 by itself.
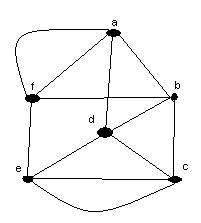
- For each of the graphs below, indicate whether the graph has
and indicate the path or the circuit if it has either one. (5 points each)
|
|
an euler path |
path or circuit
shown here if one exists |
|
|
a |
|
yes |
beabcde,
ebcdeab, ebaedcb, bedcbae, baebcde,
bcdeabe are all Euler paths |
|
b |
yes |
|
dbafadefbcecd,
abcedcefadbfa, fafbadbcecdef,fabfececbcdaf, abcecdefafbda,
cedcbdabfafec, afecbdcedafba
, afabcdbfeceda are
all Euler circuits |
a.
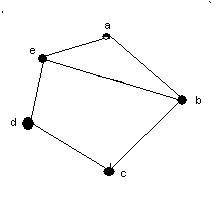
b.
12.
Given the graph below
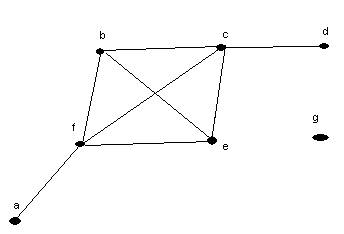
- identify each of the following (5 points)
|
isolated
vertex |
g |
|
pendant
vertex |
d or a |
|
maximum
valence |
4 |
|
number
of edges |
8 |
|
number
of vertices |
7 |
b. is the graph above connected? _No_______ Why or why not? (5 points)
No it is not connected. There is no path from any vertex to g.
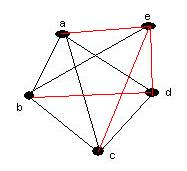
c. Add the edges to the graph below that would be needed to turn it into a complete graph? (5 points)
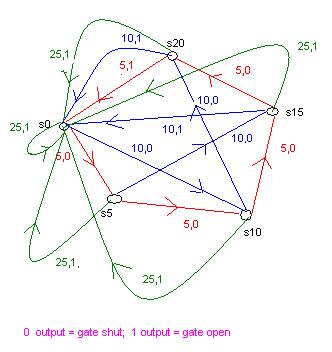
13. Show the state table or diagram (your choice) for a finite-state machine for a toll machine that opens a gate after 25 cents in nickels, dimes, or quarters has been deposited. No change is given for overpayment and no credit is given to the next driver when more than 25 cents has been deposited. (10 points)
|
Current State |
Input |
Next State |
Gate |
|
S0 |
5 |
S5 |
0 |
|
S0 |
10 |
S10 |
0 |
|
S0 |
25 |
S0 |
1 |
|
S5 |
5 |
S10 |
0 |
|
S5 |
10 |
S15 |
0 |
|
S5 |
25 |
S0 |
1 |
|
S10 |
5 |
S15 |
0 |
|
S10 |
10 |
S20 |
0 |
|
S10 |
25 |
S0 |
1 |
|
S15 |
5 |
S20 |
0 |
|
S15 |
10 |
S0 |
1 |
|
S15 |
25 |
S0 |
1 |
|
S20 |
5 |
S0 |
1 |
|
S20 |
10 |
S0 |
1 |
|
S20 |
25 |
S0 |
1 |